Tìm Hiểu Về Diện Tích Toàn Phần Hình Trụ Chuẩn Nhất

Giới Thiệu Chung Về Hình Trụ

Hình trụ là một hình khối không gian có hai đáy là hai hình tròn song song và bằng nhau, nối với nhau bằng một mặt bên uốn cong. Hình trụ là một trong những hình học cơ bản trong không gian 3 chiều và có nhiều ứng dụng trong đời sống thực tế, như trong kiến trúc, kỹ thuật, và vật lý.

Cấu tạo của hình trụ:
Hai đáy: Hình trụ có hai đáy là hai hình tròn bằng nhau và nằm song song với nhau.
Mặt bên: Là phần mặt cong nối liền giữa hai đáy, có dạng hình chữ nhật khi được "trải phẳng" ra.
Trục hình trụ: Là đoạn thẳng nối tâm của hai đáy. Trục này vuông góc với hai đáy nếu hình trụ là hình trụ đứng.
Các loại hình trụ:
Hình trụ đứng: Là hình trụ có trục vuông góc với hai đáy. Đây là loại hình trụ thường gặp và dễ hình dung nhất.
Hình trụ xiên: Là hình trụ có trục không vuông góc với hai đáy, tức là phần mặt bên sẽ bị nghiêng.
Các yếu tố cơ bản của hình trụ:
Bán kính đáy (r): Khoảng cách từ tâm của đáy đến bất kỳ điểm nào trên đường tròn của đáy.
Chiều cao (h): Khoảng cách giữa hai mặt đáy, cũng chính là độ dài của trục.
Đường sinh (l): Là đoạn thẳng nối từ một điểm bất kỳ trên đường tròn đáy này tới điểm tương ứng trên đường tròn đáy kia, song song với trục.
Ứng dụng của hình trụ:
Hình trụ xuất hiện nhiều trong cuộc sống, từ các đồ vật như lon nước ngọt, ống nước, cột trụ kiến trúc đến các bộ phận của máy móc như piston hay xi lanh.
Trong kỹ thuật và xây dựng, hình trụ cũng được sử dụng để tính toán thể tích, diện tích toàn phần hình trụ và các thuộc tính khác của các công trình như bể chứa, tháp nước.
Lưu ý đặc biệt:
Hình trụ chỉ có hai mặt đáy và một mặt bên. Mặt bên không phải là mặt phẳng mà là mặt cong khi nhìn từ ngoài vào.
Các công thức tính diện tích toàn phần hình trụ và thể tích của hình trụ thường dựa trên yếu tố chiều cao và bán kính của đáy.
Tóm lại, hình trụ là một hình học không gian cơ bản nhưng rất quan trọng, có nhiều ứng dụng trong thực tế và mang lại nhiều bài toán thú vị trong toán học.

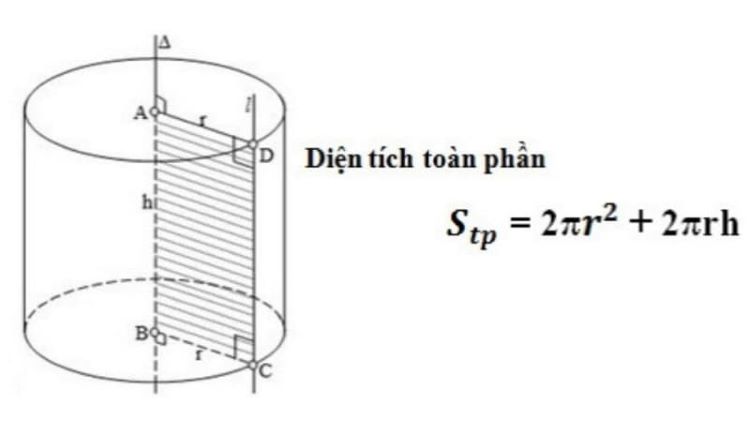
Diện tích hình trụ

Công Thức Tính Diện Tích Toàn Phần Của Hình Trụ

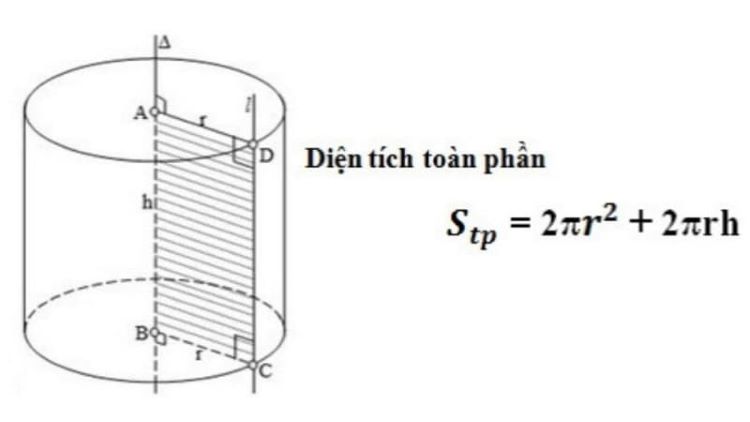
Diện tích toàn phần hình trụ chính là tổng của diện tích xung quanh và diện tích của cả hai đáy. Công thức Diện tích toàn phần hình trụ được tính như sau:

Diện tích toàn phần hình trụ

Stp = Sxq + 2 x Sđáy = 2 x π x r x h + 2 x π x r^2 = 2 x π x r x (r +h)

Stp = 2 x π x r x (r +h)

Ví dụ:

Cho hình trụ có đường kính đáy là 8dm, với chiều cao là 6dm. Hãy tính diện tích toàn phần của hình trụ này.

Theo bài ra đường kính là 8dm => bán kính r = 8/2 = 4dm

Diện tích toàn phần hình trụ là:

Stp = 2 x π x r x (r +h) = 2 x π x 4 x (4 + 6) = 80π = 251.32 dm2

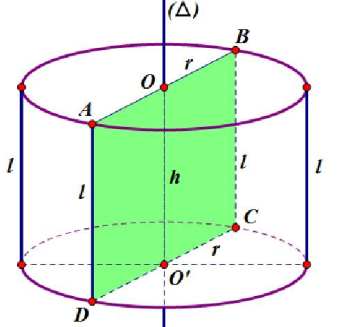
Hình trụ

Yếu Tố Ảnh Hưởng Đến Diện Tích Toàn Phần Của Hình Trụ

Các yếu tố ảnh hưởng đến diện tích toàn phần của hình trụ là những yếu tố quyết định kích thước và diện tích tổng của cả mặt bên và hai mặt đáy của hình trụ. Diện tích toàn phần của hình trụ phụ thuộc vào hai đại lượng chính: bán kính đáy (r) và chiều cao (h).
Các yếu tố ảnh hưởng trực tiếp đến diện tích toàn phần:
Bán kính đáy (r)
Bán kính đáy (r) đóng vai trò quan trọng nhất trong việc xác định diện tích toàn phần. Nó xuất hiện trong cả hai phần của công thức: diện tích đáy (2πr 2 ) và diện tích mặt bên (2πrh).
Ảnh hưởng của bán kính:
Khi bán kính r tăng, cả diện tích đáy và diện tích mặt bên đều tăng. Diện tích đáy phụ thuộc trực tiếp vào  , do đó chỉ cần thay đổi nhỏ ở bán kính cũng có thể làm diện tích toàn phần thay đổi đáng kể.
Nếu bán kính đáy tăng gấp đôi, diện tích đáy sẽ tăng lên bốn lần, trong khi diện tích mặt bên tăng theo tỉ lệ trực tiếp với bán kính.

>> Xem thêm:  Bảng đơn vị đo khối lượng

Ứng dụng vào xây dựng

 Chiều cao (h)
Chiều cao của hình trụ (h) ảnh hưởng đến diện tích mặt bên của hình trụ, vì mặt bên có diện tích được tính bằng 
2πrh.
Ảnh hưởng của chiều cao:
Khi chiều cao 
h tăng, diện tích mặt bên tăng lên, trong khi diện tích đáy vẫn giữ nguyên. Diện tích mặt bên thay đổi tuyến tính theo chiều cao, tức là nếu chiều cao tăng gấp đôi, diện tích mặt bên cũng sẽ tăng gấp đôi.
 

Sự kết hợp giữa bán kính và chiều cao
Diện tích toàn phần phụ thuộc vào cả bán kính và chiều cao của hình trụ. Sự thay đổi của một trong hai yếu tố này sẽ làm thay đổi diện tích toàn phần.
Khi cả bán kính và chiều cao tăng đồng thời, diện tích toàn phần sẽ tăng mạnh hơn
Hằng số Pi (π)
Mặc dù hằng số Pi là một giá trị cố định (
≈3.14159), nó vẫn là một phần không thể thiếu trong công thức tính diện tích toàn phần. Tuy nhiên, Pi không ảnh hưởng đến việc thay đổi diện tích theo chiều cao hoặc bán kính, vì nó là một hằng số.
Tóm lại:
Bán kính đáy (r) và chiều cao (h) là hai yếu tố quan trọng nhất ảnh hưởng đến diện tích toàn phần của hình trụ.
Bán kính có tác động lớn hơn, vì nó ảnh hưởng đến cả diện tích mặt bên và diện tích đáy.
Việc tăng hoặc giảm một trong hai yếu tố này sẽ ảnh hưởng trực tiếp đến diện tích toàn phần của hình trụ.

>> Tham khảo: Căn hộ 2 phòng ngủ Vinhomes ocean park