Nhị Thức Newton Là Gì? Cách Suy Luận Và Ghi Nhớ Hiệu Quả

Giới thiệu về nhị thức Newton

Nhị thức Newton là một công cụ toán học quan trọng trong đại số, giúp khai triển biểu thức lũy thừa của tổng hai số hạng. Công thức này mang tên nhà toán học Isaac Newton, người đã phát triển lý thuyết này vào thế kỷ XVII.

Khái niệm nhị thức Newton

Nhị thức là công thức khai triển biểu thức (a + b)^n, với n là một số nguyên không âm. Cụ thể, công thức được viết như sau:

(a + b)^n = C(n, 0) * a^n * b^0 + C(n, 1) * a^(n-1) * b^1 + ... + C(n, n) * a^0 * b^n

Hoặc viết ngắn gọn bằng tổng:

(a + b)^n = Σ [k = 0 → n] C(n, k) * a^(n - k) * b^k

Trong đó:

C(n, k) là tổ hợp chập k của n, còn gọi là hệ số nhị thức

a, b là hai số hạng trong biểu thức

n là bậc của nhị thức

Vai trò và ứng dụng

Giúp khai triển nhanh biểu thức (a + b)^n

Ứng dụng trong tổ hợp, xác suất thống kê và các thuật toán tính toán

Liên hệ với tam giác Pascal – công cụ xác định hệ số trong mỗi hàng khai triển

Hình ảnh Newton

Công thức nhị thức Newton

(a + b)^n = C(n, 0)·aⁿ·b⁰ + C(n, 1)·aⁿ⁻¹·b¹ + C(n, 2)·aⁿ⁻²·b² + ... + C(n, n)·a⁰·bⁿ

Hoặc viết gọn bằng ký hiệu tổng:

(a + b)^n = Σ [k = 0 → n] C(n, k)·aⁿ⁻ᵏ·bᵏ

Trong đó:

C(n, k) là tổ hợp chập k của n: C(n, k) = n! / (k!·(n - k)!)

a, b là hai số hạng trong biểu thức

n là số nguyên không âm

Σ là ký hiệu tổng (tổng từ k = 0 đến n)

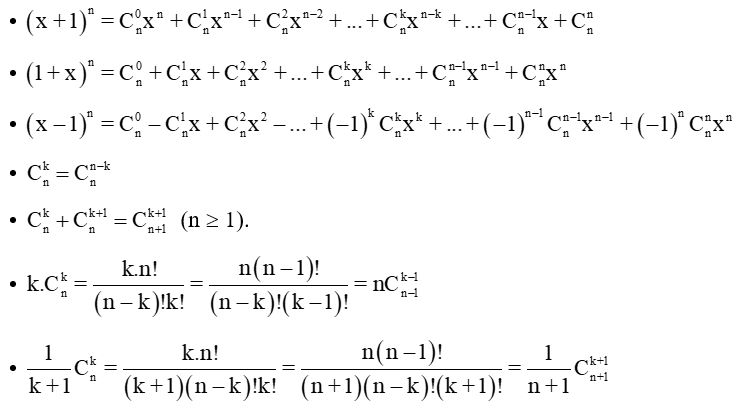
Hình ảnh khai triển công thức

Nhị thức là công cụ toán học giúp khai triển biểu thức lũy thừa của tổng hai số hạng theo một cách hệ thống và chính xác. Cụ thể, nhị thức cho phép biểu diễn biểu thức dạng:

(a + b)^n = C(n, 0)·a^n·b^0 + C(n, 1)·a^(n-1)·b^1 + ... + C(n, n)·a^0·b^n

Trong đó, C(n, k) là hệ số tổ hợp, tính theo công thức:

C(n, k) = n! / [k!(n - k)!]

Ý nghĩa của nhị thức

Giúp khai triển nhanh biểu thức (a + b)^n mà không cần nhân thủ công từng bước.

Thể hiện mối liên hệ giữa đại số và tổ hợp, từ đó làm rõ vai trò của hệ số tổ hợp trong toán học.

Đóng vai trò nền tảng trong các phép biến đổi đại số, đặc biệt khi xử lý biểu thức đa thức hoặc giải phương trình.

Ứng dụng của nhị thức

Trong toán tổ hợp: Dùng để tính nhanh số cách chọn k phần tử từ n phần tử.

Trong đại số và giải tích: Hỗ trợ tính đạo hàm, tích phân và khai triển biểu thức có lũy thừa.

Trong lập trình: Tối ưu hóa thuật toán có liên quan đến phép nhân nhiều lần hoặc tính toán tổ hợp.

Trong vật lý và kỹ thuật: Dùng trong phân tích hàm số, mô hình hóa các hệ thống hoặc phương trình chứa lũy thừa.

Nhờ tính ứng dụng rộng rãi và dễ tiếp cận, nhị thức Nwton là một phần không thể thiếu trong chương trình toán học và khoa học ứng dụng.

Học sinh trong giờ Toán

Câu hỏi thường gặp về nhị thức

Nhị thức Newton là gì?

Nhị thức Newton là công thức giúp khai triển biểu thức dạng (a + b)^n thành tổng của nhiều số hạng. Mỗi số hạng bao gồm hệ số tổ hợp, lũy thừa của a và b. Công thức này có ý nghĩa lớn trong đại số và toán tổ hợp.

Nhị thức có liên quan gì đến tam giác Pascal?

Có. Các hệ số tổ hợp trong nhị thức chính là các số nằm trong tam giác Pascal. Mỗi hàng trong tam giác Pascal tương ứng với các hệ số trong khai triển (a + b)^n.

Có thể áp dụng nhị thức Newton với số mũ âm không?

Có, nhưng khi đó ta cần mở rộng công thức thành nhị thức tổng quát dùng chuỗi vô hạn (với điều kiện |b/a| < 1). Tuy nhiên, trong chương trình phổ thông chỉ xét trường hợp số mũ nguyên không âm.