Nhị Thức Newton – Công Thức, Ý Nghĩa Và Ứng Dụng Dễ Hiểu

Khám phá nhị thức Newton, công thức khai triển, ý nghĩa toán học và ứng dụng thực tế. Bài viết chi tiết, dễ hiểu, giúp bạn học nhanh và áp dụng hiệu quả.

Nhị thức Newton

1. Công thức Newton là gì và vì sao quan trọng

Trong toán học, có những công thức không chỉ xuất hiện trong sách giáo khoa mà còn trở thành nền tảng cho rất nhiều ứng dụng khác nhau. Nhị thức Newton là một trong số đó. Đây là công thức dùng để khai triển lũy thừa của một tổng gồm hai hạng tử, được phát triển từ công trình nghiên cứu của nhà toán học vĩ đại Isaac Newton.

Nhị thức Newton không chỉ giúp giải nhanh các bài toán khai triển, rút gọn biểu thức, mà còn mở ra cách nhìn tổng quát về các hệ số tổ hợp trong toán học. Điều này khiến công thức trở thành một phần quan trọng trong chương trình phổ thông và các kỳ thi học sinh giỏi, đồng thời đóng vai trò trong nhiều lĩnh vực như xác suất thống kê, đại số, và cả khoa học máy tính.

Khái niệm cơ bản

Công thức Newton được dùng để khai triển biểu thức (a+b)n(a + b)^n thành tổng của các số hạng có dạng C(n,k)⋅an−k⋅bkC(n, k) \cdot a^{n-k} \cdot b^k, trong đó C(n,k)C(n, k) là hệ số tổ hợp. Công thức này giúp ta tránh việc nhân tay từng bước, thay vào đó áp dụng một quy tắc chuẩn xác để tìm ngay kết quả.

Vai trò trong học tập

Việc thành thạo công thức Newton không chỉ giúp giải quyết nhanh các bài tập đại số mà còn rèn luyện tư duy về quy luật và mô hình toán học. Khi hiểu được cấu trúc và ý nghĩa của từng thành phần trong công thức, bạn sẽ dễ dàng áp dụng nó vào nhiều dạng bài khác nhau, từ đơn giản đến phức tạp.

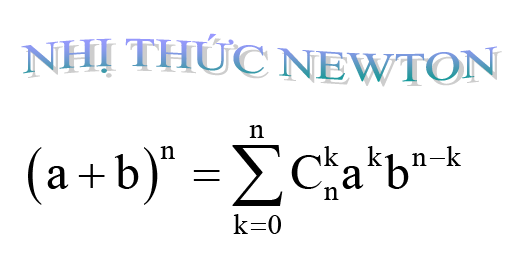
2. Lịch sử và nguồn gốc của công thức Newton

Nhị thức Newton gắn liền với tên tuổi của Isaac Newton, nhưng ý tưởng về khai triển nhị thức đã tồn tại từ trước. Vào thế kỷ 11, nhà toán học người Ba Tư Omar Khayyam đã nghiên cứu khai triển lũy thừa của tổng hai số với số mũ nguyên dương. Tuy nhiên, Newton đã mở rộng công thức này cho cả số mũ thực, mang lại một bước tiến vượt bậc.

Đóng góp của Isaac Newton

Vào thế kỷ 17, Newton đã tìm ra cách khai triển (a+b)n(a + b)^n không chỉ khi nn là số nguyên dương, mà còn cho cả số mũ âm hoặc phân số. Điều này giúp công thức trở nên toàn diện hơn và áp dụng được trong nhiều lĩnh vực của giải tích và vật lý.

Mối liên hệ với tam giác Pascal

Một điều thú vị là hệ số tổ hợp C(n,k)C(n, k) trong công thức Newton có thể được tìm ngay từ tam giác Pascal. Mỗi hàng của tam giác Pascal tương ứng với hệ số của một khai triển (a+b)n(a + b)^n. Cách tiếp cận này giúp việc ghi nhớ và tính toán trở nên trực quan, đặc biệt đối với học sinh phổ thông.

3. Công thức công thức Newton và cách sử dụng

Nhị thức Newton được viết dưới dạng:

(a+b)n=C(n,0)an+C(n,1)an−1b+C(n,2)an−2b2+...+C(n,n)bn(a + b)^n = C(n, 0)a^n + C(n, 1)a^{n-1}b + C(n, 2)a^{n-2}b^2 + ... + C(n, n)b^n

Trong đó, C(n,k)=n!/(k!(n−k)!)C(n, k) = n! / (k!(n-k)!) là hệ số tổ hợp, cho biết số cách chọn kk phần tử từ nn phần tử khác nhau.

Cách đọc và hiểu công thức

Khi khai triển (a+b)n(a + b)^n, số hạng đầu tiên luôn là ana^n và số hạng cuối cùng là bnb^n. Các số mũ của aa giảm dần từ nn xuống 0, trong khi số mũ của bb tăng dần từ 0 lên nn. Hệ số trước mỗi số hạng chính là giá trị C(n,k)C(n, k), lấy từ hàng thứ nn trong tam giác Pascal.

Ví dụ minh họa

Giả sử cần khai triển (x+2)3(x + 2)^3, áp dụng công thức Newton ta có:

(x+2)3=C(3,0)x3+C(3,1)x2(2)+C(3,2)x(22)+C(3,3)(23)(x + 2)^3 = C(3, 0)x^3 + C(3, 1)x^2(2) + C(3, 2)x(2^2) + C(3, 3)(2^3)

Kết quả: x3+6x2+12x+8x^3 + 6x^2 + 12x + 8.

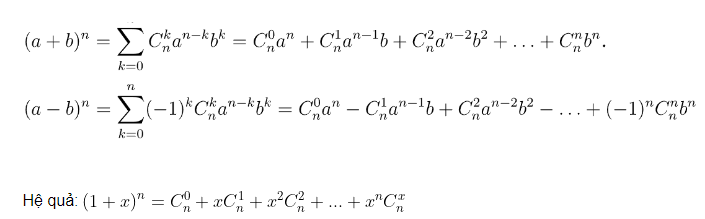
4. Ứng dụng của công thức Newton

Nhị thức Newton xuất hiện trong nhiều lĩnh vực toán học và thực tiễn. Trong xác suất thống kê, công thức được dùng để tính toán các khả năng xảy ra của sự kiện khi xét nhiều khả năng kết hợp. Trong đại số, nó giúp rút gọn và tính nhanh các biểu thức lũy thừa lớn mà không cần nhân tay từng bước.

Trong giải tích và vật lý

Khi mở rộng công thức cho số mũ thực hoặc âm, công thức Newton trở thành công cụ mạnh mẽ trong giải tích. Các bài toán về xấp xỉ giá trị, khai triển chuỗi số mũ, hay tính toán trong cơ học cổ điển đều có thể áp dụng công thức này.

Trong khoa học máy tính

Thuật toán và lập trình cũng sử dụng nguyên tắc của công thức Newton, đặc biệt trong việc phân tích độ phức tạp và thiết kế thuật toán liên quan đến tổ hợp và xác suất. Việc khai triển nhanh các biểu thức giúp tối ưu hóa thời gian tính toán.

5. Mẹo ghi nhớ và luyện tập công thức Newton

Để ghi nhớ công thức Newton hiệu quả, một cách phổ biến là sử dụng tam giác Pascal để tìm nhanh hệ số tổ hợp. Khi đã quen với mô hình này, bạn chỉ cần nhớ rằng các số mũ của aa giảm dần, của bb tăng dần, và hệ số chính là số trong tam giác Pascal tương ứng.

Việc luyện tập thường xuyên với nhiều dạng bài khác nhau cũng rất quan trọng. Bắt đầu với các số mũ nhỏ để nắm vững quy luật, sau đó thử thách bản thân với các số mũ lớn hơn. Kết hợp việc học công thức tổ hợp và công thức Newton sẽ giúp bạn giải quyết nhanh hơn các bài toán nâng cao.

Nhị thức Newton không chỉ là một công thức khai triển, mà còn là minh chứng cho sự kết nối giữa đại số, tổ hợp và nhiều lĩnh vực khoa học khác. Việc hiểu rõ công thức, nguồn gốc và ứng dụng của nó sẽ giúp bạn không chỉ học tốt môn toán mà còn rèn luyện khả năng tư duy logic và giải quyết vấn đề một cách khoa học.