Khái Niệm, Tính Chất, Công Thức Về Nhị Thức Newton.

Khái niệm cơ bản về nhị thức newton

Nhị thức Newton là một công thức trong toán học dùng để khai triển các lũy thừa của một tổng (hoặc hiệu) hai số. Công thức này rất quan trọng trong đại số và được sử dụng để mở rộng biểu thức dạng (a + b)ⁿ (hoặc (a − b)ⁿ) thành một tổng các hạng tử có chứa các lũy thừa của a và b.
Khái niệm cơ bản về nhị thức:
Công thức nhị thức cho phép khai triển biểu thức (a + b)ⁿ  theo dạng tổng các hạng tử như sau:
(a + b)ⁿ = Σ (k=0 to n) C(n, k) a^(n-k) b^k
Trong đó:
n là số mũ của biểu thức (là một số nguyên không âm).
a và b là hai số hạng trong biểu thức.
(nk) là hệ số nhị thức, hay còn gọi là hệ số Newton, được tính theo công thức tổ hợp:
(nk)= n! / (k! * (n - k)!)
Đây là số cách chọn k phần tử từ n phần tử.
k là chỉ số thay đổi từ 0 đến n, trong đó aⁿ⁻ᵏ và bᵏ là các lũy thừa của a và b.
Ví dụ:
Khi n=2, khai triển (a + b)²:
(a + b)² = (2 choose 0) a² + (2 choose 1) ab + (2 choose 2) b²
Tính toán các hệ số nhị thức:
(2/0)=1, (2/1)=2, (2/2)=1
Vậy khai triển là:
(a + b)² = a² + 2ab + b²

Khái niệm cơ bản về nhị thức new ton

Ý nghĩa của các thành phần trong công thức:
Hệ số nhị thức (n/k): Cho biết số cách chọn k phần tử từ n phần tử.
Lũy thừa aⁿ⁻ᵏ và bᵏ: Các lũy thừa này xác định số lần mỗi yếu tố aaa và bbb xuất hiện trong từng hạng tử của khai triển.
Tính chất:
Đối xứng: Hệ số nhị thức có tính đối xứng:
(n/k)= n/ n-k
Điều này có nghĩa là việc chọn k phần tử từ nnn phần tử là tương đương với việc bỏ đi n−k phần tử.

Tính chất của hệ số nhị thức newton

Hệ số nhị thức (n/k), còn gọi là hệ số tổ hợp, có nhiều tính chất quan trọng trong toán học. Dưới đây là các tính chất cơ bản của hệ số nhị thức:

Tính đối xứng:

Một trong những tính chất quan trọng của hệ số nhị thức là tính đối xứng. Cụ thể, hệ số nhị thức có tính đối xứng trong hai chỉ số k và n−k. Điều này có nghĩa là:
(n/k)=(n/n−k)
Ví dụ:
(5/2)=(5/3)
Điều này cho thấy rằng việc chọn k phần tử từ n phần tử là tương đương với việc bỏ đi n−k phần tử.

Hệ số nhị thức với k=0 và k = n:

Khi k=0 hoặc k=n, hệ số nhị thức có giá trị là 1:
(n/0)=(n/n)=1
Điều này có thể hiểu là chỉ có một cách để chọn không phần tử (hoặc chọn tất cả các phần tử) từ một tập hợp n phần tử.

Hệ số nhị thức với k=1 và k=n−1:

Khi k=1 hoặc k=n−1, hệ số nhị thức có giá trị bằng n:
(n/1)=(n/n−1)
Điều này có thể giải thích là có nnn cách chọn một phần tử từ n phần tử (hoặc chọn tất cả các phần tử trừ một).
Quan hệ với tam giác Pascal:
Hệ số nhị thức có thể được sắp xếp theo dạng tam giác Pascal, trong đó mỗi phần tử là tổng của hai phần tử ngay phía trên nó. Cụ thể:
(n/k)=(n−1/k−1)+(n−1/k)

tính chất cơ bản của hệ số nhị thức

Công thức tính hệ số nhị thức:
Hệ số nhị thức (n/k)được tính theo công thức tổ hợp:
(n/k)=n!/k!(n−k)!
Trong đó:
n! là giai thừa của n, tức là tích của tất cả các số nguyên từ 1 đến n.
k! và (n−k)! là giai thừa của k và n−k, tương ứng.
Định lý Chuẩn bị:
Có một mối quan hệ giữa các hệ số nhị thức trong các khai triển của nhị thức. Ví dụ, định lý chuẩn bị nói rằng:
(n/k)=(n−1/k−1)+(n−1/k)
Điều này có nghĩa là hệ số nhị thức có thể được tính dựa trên hai giá trị trước đó trong dòng tam giác Pascal.
Tính chất cộng và trừ:
Hệ số nhị thức có thể được sử dụng trong các phép toán cộng và trừ. Một tính chất quan trọng là:
∑k=0n(n/k)=2ⁿ
Điều này có nghĩa là tổng tất cả các hệ số nhị thức trong một hàng của tam giác Pascal là 2ⁿ.
Tính chất với số mũ:
Hệ số nhị thức (n/k) có tính chất liên quan đến sự phân bố các phần tử trong các lũy thừa của tổng, ví dụ:
(a+b)ⁿ=∑k=0n(n/k)aⁿ⁻ᵏ bᵏ
Các hệ số nhị thức xuất hiện trong khai triển này giúp xác định cách thức các yếu tố aaa và bbb kết hợp trong các lũy thừa.
Sự đối xứng trong tổ hợp:
Nhị thức cũng có một tính chất quan trọng trong lý thuyết tổ hợp: các hệ số nhị thức (n/k) thể hiện các cách chọn k phần tử từ n phần tử, và nó có tính đối xứng khi đảo ngược các chỉ số chọn:
(n/k)=(n/n−k)
Hệ số nhị thức có nhiều tính chất hữu ích trong các bài toán tổ hợp, đại số và xác suất. Những tính chất này không chỉ giúp trong việc tính toán mà còn hỗ trợ trong việc lý giải các hiện tượng toán học, đặc biệt là trong việc khai triển nhị thức và các ứng dụng trong lý thuyết xác suất và phân tích.

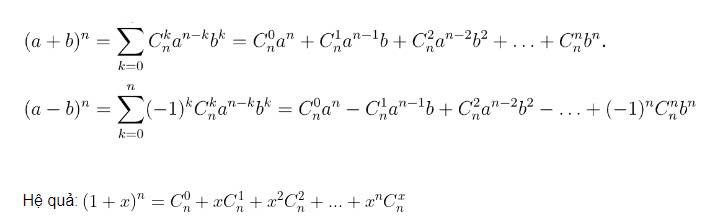
Nhị thức  có rất nhiều ứng dụng quan trọng trong toán học

Ứng dụng của Nhị thức Newton

Nhị thức  có rất nhiều ứng dụng quan trọng trong toán học, đại số, xác suất, và các lĩnh vực khoa học khác. Dưới đây là một số ứng dụng chính của Nhị thức :
Khai triển các lũy thừa của tổng:
Nhị thức  cho phép khai triển các biểu thức dạng (a+b)ⁿ thành một tổng các hạng tử, mỗi hạng tử bao gồm một lũy thừa của a và b. Đây là ứng dụng cơ bản và quan trọng nhất của nhị thức trong đại số.
Ứng dụng này được sử dụng rộng rãi trong việc giải quyết các bài toán đại số, đặc biệt khi cần mở rộng một biểu thức phức tạp thành các hạng tử đơn giản hơn.
Ứng dụng trong xác suất và lý thuyết xác suất:
Nhị thức  có ứng dụng quan trọng trong lý thuyết xác suất, đặc biệt là trong các bài toán liên quan đến phân phối nhị thức. Phân phối nhị thức mô tả xác suất của các sự kiện trong các thử nghiệm Bernoulli (thử nghiệm có hai kết quả có thể xảy ra, như "thành công" hoặc "thất bại").
Trong các bài toán xác suất, nhị thức giúp tính toán số cách sắp xếp các kết quả có thể xảy ra trong các thử nghiệm và tính toán xác suất tương ứng.
Tính toán chuỗi Taylor và khai triển hàm:
Nhị thức  cũng được sử dụng trong việc khai triển các hàm số thành chuỗi Taylor. Chuỗi Taylor là một công cụ mạnh mẽ trong phân tích hàm, giúp xấp xỉ các hàm số phức tạp bằng các đa thức bậc cao.
Ứng dụng trong đại số tuyến tính:
Nhị thức  cũng có ứng dụng trong đại số tuyến tính, đặc biệt là trong việc tính toán các ma trận và các lũy thừa của ma trận. Khi tính lũy thừa của một ma trận (A+B)ⁿ, ta có thể áp dụng nhị thức để mở rộng và tính toán các hạng tử của biểu thức này.
Điều này rất hữu ích trong các bài toán về ma trận và lý thuyết ma trận, như tính toán các ma trận lớn hoặc trong các bài toán giải phương trình ma trận.
 Ứng dụng trong phân tích số:
Trong các bài toán phân tích số và tối ưu hóa, nhị thức giúp xấp xỉ các giá trị và tính toán các hàm số phức tạp. Việc khai triển nhị thức giúp làm đơn giản hóa các bài toán bằng cách chia chúng thành các bước nhỏ hơn hoặc các hàm đơn giản hơn.
Ứng dụng trong lý thuyết đồ thị:
Nhị thức có thể được sử dụng trong lý thuyết đồ thị, đặc biệt là khi tính toán các thuộc tính của đồ thị, như số cách chọn các đỉnh hoặc cạnh từ đồ thị. Hệ số nhị thức cũng có thể giúp tính toán các số liệu liên quan đến các đường đi hoặc chu trình trong đồ thị.
Ứng dụng trong công thức xác suất kết hợp (Combinatorics):
Nhị thức  là công cụ quan trọng trong lý thuyết tổ hợp (combinatorics). Hệ số nhị thức (n/k) đại diện cho số cách chọn kkk phần tử từ một tập hợp n phần tử mà không quan tâm đến thứ tự. Đây là công thức cơ bản để giải quyết nhiều bài toán tổ hợp liên quan đến việc phân phối, xếp hạng, hoặc lựa chọn các đối tượng trong tập hợp.
Ứng dụng trong các phương pháp tính toán xấp xỉ:
Nhị thức  cũng giúp trong việc xây dựng các phương pháp tính toán xấp xỉ, như trong phương pháp phân tích xấp xỉ Newton-Raphson. Phương pháp này được sử dụng để tìm nghiệm của một phương trình bằng cách sử dụng các giá trị gần đúng.
Ứng dụng trong lý thuyết số và phân tích phân số:
Nhị thức  cũng xuất hiện trong lý thuyết số, đặc biệt trong các bài toán liên quan đến phân tích phân số hoặc mở rộng các biểu thức có dạng phân số (ví dụ như các chuỗi phân số hoặc hàm số liên quan đến phân số).

Kết luận

Nhị thức là một công cụ rất mạnh mẽ và linh hoạt trong toán học, với các ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, từ đại số, lý thuyết xác suất, đến phân tích hàm và lý thuyết tổ hợp.
Bài viết trên đã giới thiệu về Nhị thức, từ khái niệm cơ bản, các tính chất quan trọng cho đến những ứng dụng đa dạng của nó trong toán học và các lĩnh vực khác như lý thuyết xác suất, tổ hợp, và đại số tuyến tính. Hy vọng rằng qua bài viết này, bạn đọc sẽ hiểu rõ hơn về công thức nhị thức , tầm quan trọng của nó trong việc giải quyết các bài toán phức tạp, cũng như ứng dụng của nó trong thực tế. Nhị thức không chỉ là một công cụ lý thuyết mà còn là nền tảng giúp phát triển nhiều phương pháp tính toán và giải quyết vấn đề trong các ngành khoa học và kỹ thuật.
Để nhận được tư vấn về các dịch vụ do VINHOMES MIỀN BẮC cung cấp, vui lòng liên hệ qua Hotline: 0943.238.228 hoặc Email: duytran1185@gmail.com để nhận được tư vấn trực tiếp từ phía chuyên viên.