Hướng Dẫn Cách Tính Diện Tích Toàn Phần Hình Trụ Dễ Hiểu

Hình trụ là một hình khối không gian quen thuộc, xuất hiện rất nhiều trong thực tế như lon nước ngọt, ống nhựa, trụ cột nhà,... Về mặt hình học, hình trụ được tạo thành khi quay một hình chữ nhật quanh một cạnh cố định. Khi đó, hai mặt đáy của hình trụ là hai hình tròn bằng nhau và song song, mặt còn lại gọi là mặt xung quanh.

Diện tích toàn phần của hình trụ là tổng diện tích của toàn bộ bề mặt hình trụ, bao gồm:

Diện tích mặt xung quanh

Diện tích hai đáy

Việc tính diện tích hình trụ giúp chúng ta biết được lượng vật liệu cần dùng để bọc hoặc sơn phủ toàn bộ hình trụ trong các bài toán thực tế, kỹ thuật hoặc sản xuất.

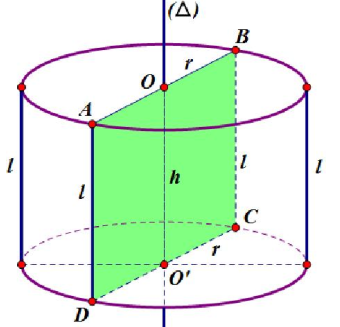
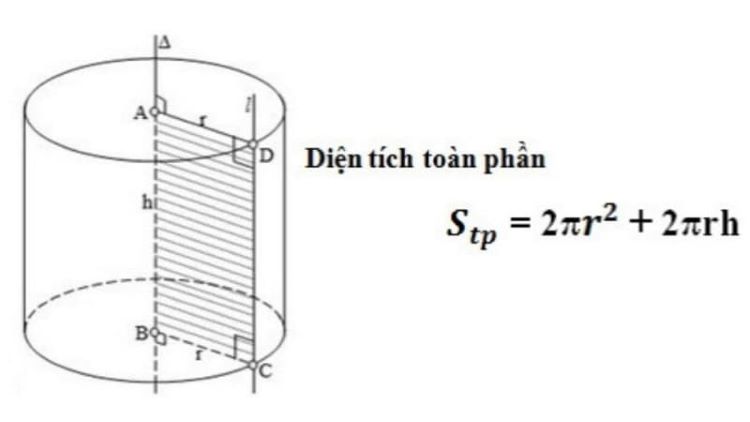
Hình trụ

Trước khi tính diện tích toàn phần, ta cần xác định các yếu tố cơ bản của hình trụ:

r: bán kính đáy hình trụ

h: chiều cao hình trụ

π: số Pi, xấp xỉ 3.14 (hoặc để nguyên dạng π)

Công thức diện tích toàn phần của hình trụ được tính như sau:

Diện tích toàn phần (S_tp) = Diện tích xung quanh + Diện tích 2 đáy

→ S_tp = 2πrh + 2πr²

Trong đó:

2πrh là diện tích mặt xung quanh

2πr² là diện tích hai đáy

Ví dụ minh họa:

Cho hình trụ có bán kính đáy r = 5 cm và chiều cao h = 10 cm. Hãy tính diện tích toàn phần.

Áp dụng công thức:

S_tp = 2πrh + 2πr²

S_tp = 2 × π × 5 × 10 + 2 × π × 5²

S_tp = 100π + 50π = 150π ≈ 471 cm²

Kết luận: Diện tích hình trụ là khoảng 471 cm².

Công thức được áp dụng trong nhiều lĩnh vực

Việc tính diện tích toàn phần không chỉ xuất hiện trong bài tập Toán mà còn có nhiều ứng dụng thực tế trong đời sống và công nghiệp:

Khi thiết kế vỏ lon nước ngọt, người ta cần biết diện tích giấy hoặc nhôm để bọc toàn bộ thân lon – chính là diện tích toàn phần hình trụ.

Khi cần sơn một chiếc ống nước hoặc trụ cột tròn, người ta dùng công thức tính diện tích toàn phần để biết chính xác lượng sơn cần dùng.

Trong thiết kế cột tròn, cột bê tông, kiến trúc sư tính toán diện tích toàn phần để dự trù vật liệu và chi phí.

Bài toán hình trụ thường có trong chương trình học lớp 9 và lớp 12, giúp học sinh hiểu được mối liên hệ giữa hình học không gian và đời sống.

Để ghi nhớ công thức tính diện tích toàn phần của hình trụ nhanh chóng, bạn có thể áp dụng một số mẹo sau:

Diện tích mặt xung quanh: 2πrh → hình chữ nhật quấn quanh hình trụ

Diện tích hai đáy: 2πr² → vì có 2 mặt đáy hình tròn

Tổng lại: S_tp = 2πrh + 2πr²

Dùng câu nói dễ nhớ:

"Hai Pi r h + hai Pi r bình" → vần điệu đơn giản, dễ thuộc

Mặt xung quanh như tờ giấy quấn quanh hình trụ

Hai đáy là hai hình tròn trên và dưới

→ Tổng diện tích chính là bọc hết toàn bộ bề mặt

Thực hành nhiều bài tập:

Làm bài tập từ dễ đến khó, thay đổi r và h liên tục

So sánh giữa diện tích xung quanh và diện tích toàn phần để hiểu rõ bản chất

Diện tích toàn phần hình trụ là kiến thức quan trọng trong chương trình Toán học và có nhiều ứng dụng thực tế. Nắm vững công thức S_tp = 2πrh + 2πr² sẽ giúp bạn giải nhanh các bài toán về hình học không gian cũng như hiểu cách vận dụng trong sản xuất, xây dựng và thiết kế.

Đừng quên luyện tập nhiều dạng bài, vẽ hình minh họa và sử dụng các mẹo ghi nhớ để công thức trở nên thân thuộc với bạn. Khi đã hiểu bản chất và có sự liên tưởng thực tế, việc học hình trụ nói riêng và hình học không gian nói chung sẽ trở nên dễ dàng và thú vị hơn rất nhiều.