Kiến Thức Hữu Ích
Đường trung tuyến là gì? Giải thích chi tiết kèm ví dụ minh họa
1/15/2026 7:15:00 PM
5/5 - (0
Bình chọn )
Đường trung tuyến là gì
1.Đường trung tuyến là gì trong hình học?
Đường trung tuyến là gì? Trong hình học, đường trung tuyến là đoạn thẳng nối từ một đỉnh của tam giác đến trung điểm của cạnh đối diện. Nói cách khác, đường trung tuyến chia cạnh đối diện thành hai phần bằng nhau và luôn đi từ đỉnh tam giác đến chính giữa cạnh đối diện đó.
Một số đặc điểm quan trọng của đường trung tuyến:
Mỗi tam giác có ba đường trung tuyến, xuất phát từ mỗi đỉnh.
Ba đường trung tuyến đồng quy tại một điểm duy nhất gọi là trọng tâm, là điểm cân bằng của tam giác.
Trọng tâm chia mỗi đường trung tuyến theo tỉ lệ 2:1, tính từ đỉnh đến trung điểm cạnh đối diện.
Đường trung tuyến là gì? Ví dụ minh họa:
Trong tam giác ABC, D là trung điểm của BC. Khi đó, AD là đường trung tuyến của tam giác ABC.
Đường trung tuyến là kiến thức cơ bản nhưng rất quan trọng trong hình học, đặc biệt khi tính diện tích, trọng tâm hoặc giải các bài toán liên quan đến tam giác.
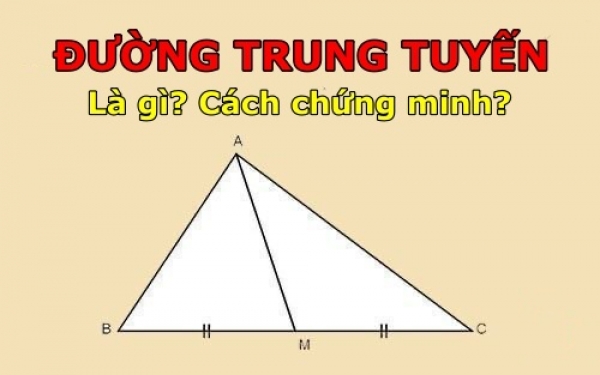
Định nghĩa đường trung tuyến
2.Cách vẽ đường trung tuyến trong tam giác như thế nào?
Đường trung tuyến trong tam giác là đoạn thẳng nối từ một đỉnh đến trung điểm của cạnh đối diện. Việc vẽ đường trung tuyến khá đơn giản, bạn chỉ cần làm theo các bước sau:
Bước 1: Xác định tam giác
Vẽ tam giác ABC bất kỳ trên giấy.
Ghi rõ các đỉnh A, B, C.
Bước 2: Xác định trung điểm của cạnh đối diện
Chọn một đỉnh mà bạn muốn vẽ đường trung tuyến từ đó, ví dụ đỉnh A.
Tìm trung điểm D của cạnh đối diện BC. Trung điểm là điểm chia cạnh thành hai phần bằng nhau, tức BD = DC.
Bạn có thể dùng thước đo hoặc compa để xác định chính xác trung điểm.
Bước 3: Nối đỉnh với trung điểm
Vẽ một đường thẳng từ đỉnh A đến trung điểm D.
Đường thẳng này chính là đường trung tuyến AD của tam giác ABC.
Bước 4: Vẽ các đường trung tuyến khác (tùy chọn)
Tương tự, bạn có thể vẽ từ đỉnh B đến trung điểm của AC, từ đỉnh C đến trung điểm của AB.
Khi vẽ đủ ba đường trung tuyến, bạn sẽ thấy chúng đồng quy tại trọng tâm G của tam giác.
📌 Mẹo:
Khi muốn vẽ chính xác, dùng thước đo hoặc compa để xác định trung điểm.
Ghi chú trọng tâm G nếu vẽ cả ba đường trung tuyến: trọng tâm chia mỗi đường trung tuyến theo tỉ lệ 2:1, tính từ đỉnh đến trung điểm cạnh đối diện.
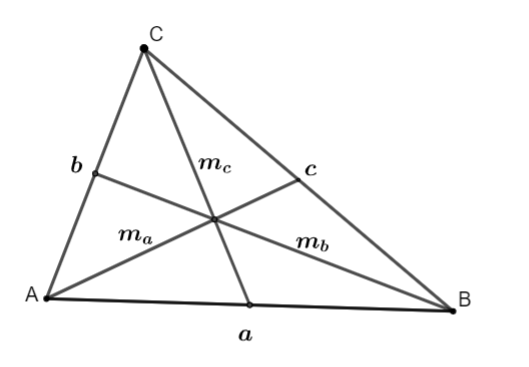
Cách vẽ đường trung tuyến trong tam giác
3.Bài tập tính đường trung tuyến có lời giải chi tiết?
Dưới đây là ví dụ bài tập tính đường trung tuyến trong tam giác kèm lời giải chi tiết:
Bài tập 1:
Đề bài:
Cho tam giác ABC có độ dài các cạnh:
AB = 6, AC = 8, BC = 10
Tính độ dài đường trung tuyến từ đỉnh A đến trung điểm D của cạnh BC.
Lời giải:
Công thức tính đường trung tuyến từ đỉnh A đến trung điểm D của cạnh đối diện BC:
AD = (1/2) × √(2AB² + 2AC² − BC²)
Thay số vào:
AD = (1/2) × √(2×6² + 2×8² − 10²)
= (1/2) × √(72 + 128 − 100)
= (1/2) × √100
= 10 / 2
= 5
Kết luận:
Đường trung tuyến AD = 5 đơn vị.
Bài tập 2:
Đề bài:
Tam giác DEF có các cạnh:
DE = 7, DF = 9, EF = 10
Tính độ dài đường trung tuyến từ đỉnh D đến trung điểm M của cạnh EF.
Lời giải:
Công thức:
DM = (1/2) × √(2DE² + 2DF² − EF²)
Thay số:
DM = (1/2) × √(2×7² + 2×9² − 10²)
= (1/2) × √(98 + 162 − 100)
= (1/2) × √160
= (1/2) × 4√10
= 2√10 ≈ 6,32
Kết luận:
Đường trung tuyến DM ≈ 6,32 đơn vị.
4.Mẹo học thuộc và nhận biết đường trung tuyến nhanh chóng?
Dưới đây là một số mẹo học thuộc và nhận biết đường trung tuyến trong tam giác nhanh chóng, viết chi tiết để học sinh dễ nhớ và áp dụng:
Nhớ định nghĩa đơn giản
Đường trung tuyến là đoạn thẳng nối từ một đỉnh của tam giác đến trung điểm của cạnh đối diện.
Mẹo: “Trung tuyến đi từ đỉnh tới trung điểm” → cứ nhìn vào đỉnh và cạnh đối diện là nhận ra ngay.
Nhận biết bằng quan sát trong hình vẽ
Mỗi tam giác có ba đường trung tuyến, xuất phát từ mỗi đỉnh.
Đường trung tuyến luôn chia cạnh đối diện thành hai phần bằng nhau.
Mẹo: Khi nhìn tam giác, hãy xác định trung điểm của cạnh trước, rồi nối với đỉnh → đường nối đó là trung tuyến.
Ghi nhớ trọng tâm
Ba đường trung tuyến đồng quy tại trọng tâm (G).
Mẹo: Nếu vẽ được trọng tâm, bạn sẽ nhanh chóng nhận ra tất cả các đường trung tuyến đều đi qua điểm này.
Dùng công thức Apollonius để nhớ độ dài
Công thức:
AD = 1/2 × √(2×AB² + 2×AC² − BC²)
Mẹo: “2AB² + 2AC² − BC², chia 2 và lấy căn” → nhớ nhanh cách tính độ dài trung tuyến.
Thực hành bằng bài tập vẽ và tính toán
Vẽ tam giác bất kỳ, tìm trung điểm các cạnh, nối với đỉnh → bạn sẽ nhận diện nhanh đường trung tuyến.
Tính độ dài đường trung tuyến bằng công thức Apollonius → ghi nhớ công thức qua ví dụ thực tế.
Sử dụng hình ảnh minh họa và flashcard
Vẽ tam giác, đánh dấu trung điểm và đường trung tuyến → giúp học sinh ghi nhớ trực quan.
Flashcard: Mặt trước: “Đỉnh A → Trung điểm BC”, mặt sau: “Đường trung tuyến AD” → học nhanh, nhớ lâu.
📌 Tóm lại:
Để học và nhận biết đường trung tuyến nhanh:
Nhớ định nghĩa cơ bản
Nhìn hình vẽ và xác định trung điểm
Ghi nhớ trọng tâm và đặc điểm đồng quy
Thực hành vẽ và tính toán
Sử dụng hình minh họa và flashcard
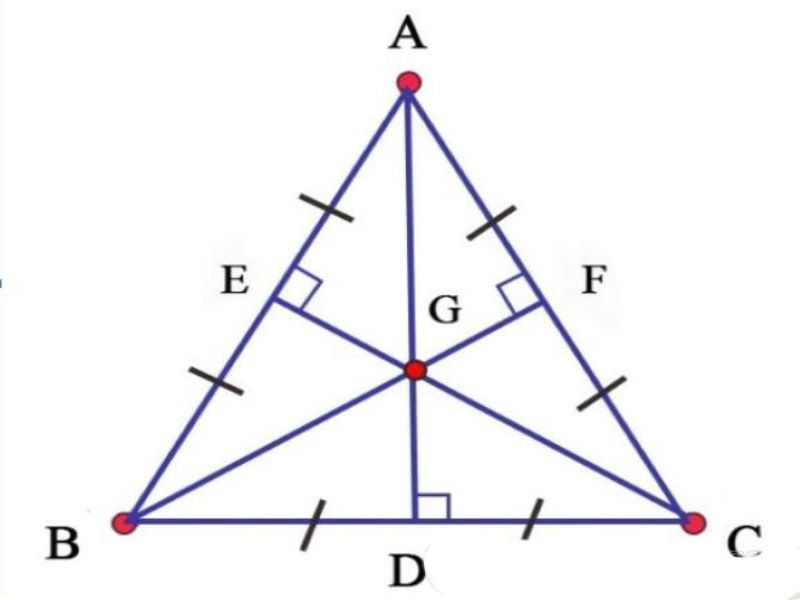
Bài tập áp dụng về đường trung tuyến
5.Ứng dụng thực tế của đường trung tuyến trong đo đạc và xây dựng?
Đường trung tuyến không chỉ là khái niệm lý thuyết trong hình học, mà còn có nhiều ứng dụng thực tế quan trọng trong đo đạc, kiến trúc và xây dựng:
Xác định trọng tâm của tam giác trong kiến trúc
Trọng tâm là điểm đồng quy của ba đường trung tuyến, giúp xác định trung tâm cân bằng của tam giác.
Trong thiết kế nhà, cầu, mái che tam giác hay các công trình hình học, việc tìm trọng tâm giúp cân bằng lực, bố trí hợp lý và đảm bảo ổn định kết cấu.
Chia tam giác thành các phần bằng nhau hoặc tỷ lệ chuẩn
Đường trung tuyến chia cạnh đối diện thành hai phần bằng nhau, giúp xác định các điểm chính giữa, lập lưới đo đạc hoặc chia mảnh đất hình tam giác thành các phần nhỏ.
Ứng dụng trong đo đất, lập bản đồ hoặc xây dựng sân vườn, công viên tam giác.
Hỗ trợ đo khoảng cách và định vị trong xây dựng
Khi cần vẽ, đo hoặc dựng tam giác chính xác, đường trung tuyến giúp xác định các điểm quan trọng mà không cần đo trực tiếp toàn bộ cạnh.
Ví dụ: Xác định điểm trung tâm trụ, cột hoặc móng nhà dựa vào trọng tâm tam giác.
Tối ưu hóa bố cục và thẩm mỹ
Trong kiến trúc và thiết kế cảnh quan, đường trung tuyến giúp đặt vật thể, trụ, hòn non bộ, cây cối… theo tỷ lệ cân đối.
Nhờ đó, bố cục hài hòa, cân đối và thẩm mỹ hơn, đồng thời tính toán lực tác động chính xác.
Ứng dụng trong kỹ thuật và cơ học
Trong kỹ thuật cơ khí, đường trung tuyến của tam giác dùng để tính toán trọng tâm tam giác của vật liệu hoặc tính lực tác động đồng đều lên cấu kiện.
Trên đây, chúng tôi đã giải thích chi tiết về đường trung tuyến là gì, cách vẽ, công thức tính độ dài, bài tập minh họa có lời giải và các mẹo học nhanh. Hy vọng bài viết Đường trung tuyến là gì
sẽ giúp bạn hiểu rõ kiến thức, áp dụng chính xác trong học tập và thực tế, đồng thời ghi nhớ công thức và cách nhận biết đường trung tuyến một cách dễ dàng.