Diện Tích Xung Quanh, Diện Tích Toàn Phần Hình Trụ Chi Tiết Nhất

 

Công thức tính Diện tích hình trụ bao gồm diện tích xung quanh và diện tích toàn phần. Vậy cụ thể công thức tính Diện tích toàn phần hình trụ ra sao, cách áp dụng như nào? Cùng tìm hiểu chi tiết trong bài viết dưới đây.

Khái niệm về hình trụ

Hình trụ là một trong các hình học không gian cơ bản. Nó được giới hạn bởi mặt trụ và hai đáy là hai đường tròn bằng nhau. Về bản chất, hình trụ thẳng tròn xoay được tạo ra bằng cách quay hình chữ nhật quanh một cạnh cố định. Giả sử hình chữ nhật có tên là ABCD, xoay quanh CD là một cạnh cố định, khi đó:

- DA và AB sẽ quét nên hai đáy của hình trụ, là hai hình tròn bằng nhau và song song nhau, tâm hai đường tròn lần lượt là D và C.

- Mặt xung quanh của hình trụ sẽ được quét lên bởi cạnh AB. Mỗi vị trí của AB sẽ được gọi là một đường sinh.

- Các đường sinh sẽ vuông góc với hai mặt phẳng đáy (2 hình tròn).

- Độ cao của hình trụ chính là độ dài của trục hình trụ (cạnh DC) hoặc chính bằng độ dài đường sinh.

Các công thức tính diện tích hình trụ

Công thức diện tích xung quanh của hình trụ

Diện tích xung quanh hình trụ được tính theo công thức như sau:

Sxq = 2 x π x h x r

Trong đó:

Sxq là diện tích xung quanh hình trụ

π là hằng số Pi (xấp xỉ 3.14159)

r là bán kính của hình tròn đáy

h là chiều cao của hình trụ

Ví dụ:

Cho hình trụ có bán kính mặt đáy r = 3cm, với chiều bao h = 5cm. Hãy tính diện tích xung quanh của hình trụ đó.

Sxq = 2 x π x r x h = 2 x π x 3 x 5 = 30π = 94.25 (cm2)

 

Công thức diện tích toàn phần hình trụ

Diện tích toàn phần hình trụ chính là tổng của diện tích xung quanh và diện tích của cả hai đáy. Công thức Diện tích toàn phần hình trụ được tính như sau:

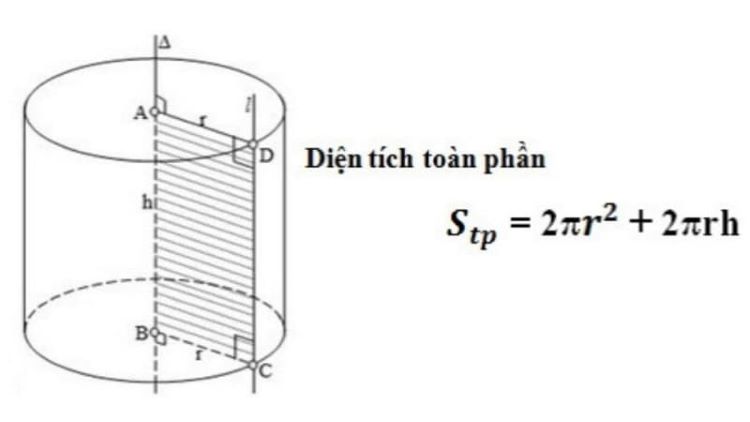
Diện tích toàn phần hình trụ

Stp = Sxq + 2 x Sđáy = 2 x π x r x h + 2 x π x r^2 = 2 x π x r x (r +h)

Stp = 2 x π x r x (r +h)

Ví dụ:

Cho hình trụ có đường kính đáy là 8dm, với chiều cao là 6dm. Hãy tính diện tích toàn phần của hình trụ này.

Theo bài ra đường kính là 8dm => bán kính r = 8/2 = 4dm

Diện tích toàn phần hình trụ là:

Stp = 2 x π x r x (r +h) = 2 x π x 4 x (4 + 6) = 80π = 251.32 dm2

>> Xem thêm: Bảng đơn vị đo khối lượng

Các dạng bài tập liên quan đến diện tích hình trụ

Dạng 1: Tính chiều cao của hình trụ

Ví dụ:

Diện tích xung quanh của 1 hình trụ là 94.2cm2 với bán kính đáy r = 3cm. Tính chiều cao ℎ của hình trụ.

Giải: 

Áp dụng công thức diện tích xung quanh S=2 x π x r x h giải ra để tìm ra h.

94.2=2 x π x 3 x h  ⟹  h = 94.2/(6π) ​≈ 5cm

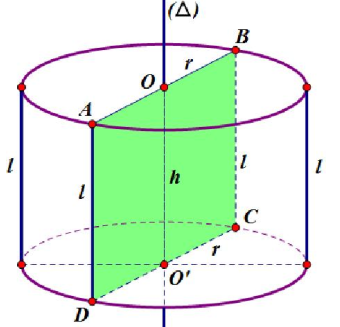
Các bài tập liên quan đến diện tích hình trụ

Dạng 2: Tính bán kính đáy của hình trụ

Ví dụ:

Cho 1 hình trụ có diện tích xung quanh Sxq là 125.6cm2 và chiều cao h=4cm. Tính bán kính r của đáy.

Giải: 

Sử dụng công thức Sxq = 2 x π x r x h để tìm ra r.

=> 125.6 = 2 x π x r x 4⟹ r = 125.6/(8 x π) ​≈ 5cm

Dạng 3: Cho Đáy là đường tròn ngoại tiếp tam giác, tính diện tích hình trụ

Đề bài:

Cho hình trụ có chiều cao h là 8cm, bán kính đáy r là bán kính của đường tròn ngoại tiếp tam giác ABC có các cạnh lần lượt là a = 3cm, b = 4cm, c = 5cm. Tính diện tích toàn phần của hình trụ.

Giải: 

Trước hết cần áp dụng công thức tính bán kính đường tròn ngoại tiếp: 

r=abc/√((a+b+c)(a+b−c)(a−b+c)(−a+b+c))​

Thay a = 3, b = 4, c = 5 để tìm r bằng bao nhiêu?

Sau khi tính được r, ta áp dụng công thức tính diện tích toàn phần của hình trụ: Stp = 2 x π x r x (r +h)

Dạng 4: Đáy là đường tròn nội tiếp tam giác, tính diện tích hình trụ.

Ví dụ: 

Cho Tam giác ABC có các cạnh a=3cm,b=4cm,c=5cm và diện tích tam giác S=6cm2. Đường tròn nội tiếp tam giác này là đáy của 1 hình trụ có chiều cao h là 8cm. Tính diện tích xung quanh của hình trụ nêu trên.

Giải:

Để tính bán kính đường tròn nội tiếp, ta áp dụng công thức sau: r = S/((a+b+c​)/2)​

Thay a = 3, b = 4, c = 5 và S = 6 vào công thức trên để tính r.

Sau khi tính được r. Ta áp dụng công thức tính diện tích xung quanh hình trụ: 

Sxq = 2 x π x r x h

 

Bài toán ứng dụng diện tích hình trụ thực tế

Bài 1: Tính diện tích vật liệu để làm thùng nước

Đề bài:

Một công ty phải sản xuất thùng nước có dạng hình trụ có chiều cao 1.5 mét với đường kính đáy là 1 mét. TÍnh diện tích vật liệu cần thiết để làm thùng nước này mà không tính nắp đậy.

Giải

Ta có: Bán kính đáy của thùng nước: r = 1/2​m= 0.5m

Chiều cao: h = 1.5m

Áp dụng công thức diện tích xung quanh hình trụ (không tính nắp đậy): 

Sxq = 2 x π x r x h = 2 x π x 0.5 x 1.5

<=>Sxq = 4.71 m2

Bài 2: Tính diện tích giấy để bọc làm pháo hoa

Đề bài:

Một công ty chuyên sản xuất pháo hoa cần bọc ngoại quan của pháo hoa hình trụ bằng giấy. Pháo hoa có chiều cao là 30 cm với bán kính đáy là 5 cm. Tính diện tích giấy cần thiết để bọc trọn pháo hoa này.

Hướng dẫn giải:

Theo bài ra ta có: 

Bán kính đáy: r = 5cm

Chiều cao: h = 30cm

Diện tích giấy cần thiết: Sxq = 2 x π x r x h = 2 x π x 5 x 30 = 942.48cm2

Bài 3: Tính diện tích mặt vải để làm cột trang trí

Đề bài:

Cột trang trí trong một sự kiện cần được bọc lại bằng vải. Cột có hình dáng của một hình trụ với chiều cao 3 mét cùng bán kính đáy 20 cm. Hãy tính diện tích mét vải cần để bọc cột trang trí này.

Giải

Theo bài ra ta có: 

Bán kính đáy: r = 20cm = 0.2m

Chiều cao: h = 3m

Vậy Diện tích vải cần thiết: 

S = 2 x π x r x h = 2 x π x 0.2 x 3 ≈3.77m2

Trên đây là toàn bộ những thông tin chi tiết về diện tích toàn trụ hình trụ. Hy vọng qua bài viết đã cho bạn những cái nhìn tổng quan về công thức tính và cách áp dụng sao cho đúng.

>> Tham khảo: Biệt thự song lập Vinhomes Ocean Park