Công Thức Tính Diện Tích Toàn Phần Hình Trụ Và Những Ví Dụ
Diện tích toàn phần hình trụ
Diện tích toàn phần của hình trụ là gì?
Diện tích toàn phần của hình trụ là tổng diện tích của tất cả các bề mặt của hình trụ, bao gồm:
- Diện tích của hai mặt đáy: Hình trụ có hai mặt đáy hình tròn. Diện tích mỗi mặt đáy là pi r^2, với r là bán kính của đáy.
- Diện tích mặt bên: Mặt bên của hình trụ là một hình chữ nhật khi mở ra. Diện tích của mặt bên là chu vi đáy nhân với chiều cao. Chu vi của đáy là 2πr và chiều cao của hình trụ là h. Do đó, diện tích mặt bên là 2πrh.
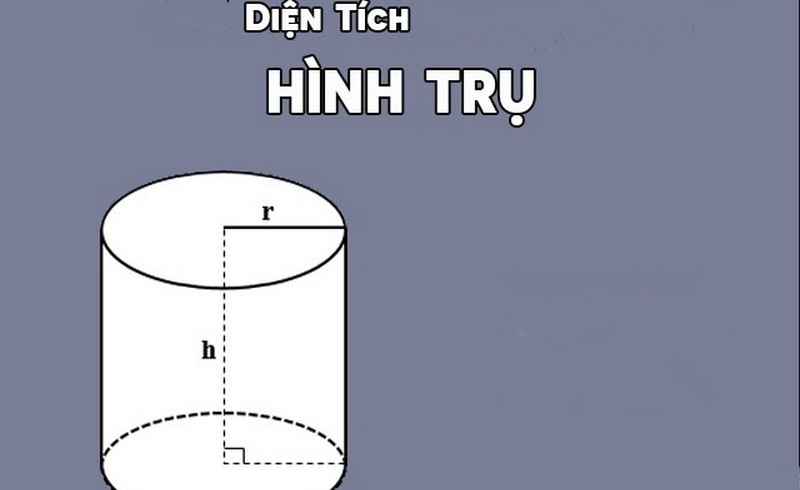
Diện tích hình trụ
Các công thức liên quan đến hình trụ
Dưới đây là các công thức cơ bản và liên quan đến hình trụ:
Diện Tích Toàn Phần Hình Trụ:
Công thức: A=2πr^2 + 2πrh
Trong đó:
r là bán kính của mặt đáy.
h là chiều cao của hình trụ.
Công thức này tính tổng diện tích của hai mặt đáy và mặt xung quanh (mặt bên) của hình trụ.
Diện Tích Mặt Đáy của Hình Trụ:
Công thức: Ađaˊy=πr^2
Trong đó:
r là bán kính của mặt đáy.
Đây là diện tích của một mặt đáy, vì hình trụ có hai mặt đáy.
Diện Tích Mặt Xung Quanh (Mặt Bên) của Hình Trụ:
Công thức: Abên=2πrh
Trong đó:
r là bán kính của mặt đáy.
h là chiều cao của hình trụ.
Đây là diện tích của phần mặt bên quanh hình trụ.
Thể Tích của Hình Trụ:
Công thức: V=πr^2 h
Trong đó:
r là bán kính của mặt đáy.
h là chiều cao của hình trụ.
Công thức này tính thể tích không gian bên trong hình trụ.
Đường Kính của Hình Trụ:
Công thức: d=2r
Trong đó:
r là bán kính của mặt đáy.
Đường kính là gấp đôi bán kính.
Chu Vi Mặt Đáy của Hình Trụ:
Công thức: C=2πr
Trong đó:
r là bán kính của mặt đáy.
Công thức này tính chu vi của mặt đáy hình trụ, là vòng tròn quanh bán kính.
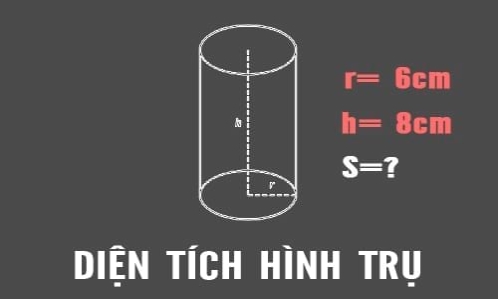
Công thức tính diện tích hình trụ
Chiều Cao của Hình Trụ Khi Biết Thể Tích và Diện Tích Toàn Phần:
Công thức: h=V / π r^2
Trong đó:
V là thể tích của hình trụ.
r là bán kính của mặt đáy.
Bán Kính Khi Biết Thể Tích và Diện Tích Toàn Phần:
Công thức:
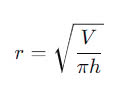
Trong đó:
V là thể tích của hình trụ.
h là chiều cao của hình trụ.
Diện Tích Toàn Phần khi biết đường kính và chiều cao:
Công thức: A=πd^2 + πd2
Trong đó:
d là đường kính của mặt đáy.
h là chiều cao của hình trụ.
Những công thức này giúp bạn tính toán các thuộc tính khác nhau của hình trụ, từ diện tích và thể tích cho đến các đặc điểm như đường kính và chu vi.
>> Xem thêm: Số nguyên tố là gì
Tác dụng của diện tích toàn phần hình trụ
Diện tích toàn phần của hình trụ có nhiều tác dụng quan trọng trong các lĩnh vực khác nhau, từ thiết kế và chế tạo đến ứng dụng trong đời sống hàng ngày. Dưới đây là một số tác dụng chính của diện tích toàn phần hình trụ:
Thiết Kế và Chế Tạo Vật Dụng:
Chai và Bình: Biết diện tích toàn phần của chai hoặc bình giúp trong việc thiết kế và sản xuất các sản phẩm đựng nước, thực phẩm, và các chất lỏng khác. Diện tích toàn phần ảnh hưởng đến số lượng vật liệu cần thiết và thiết kế bao bì.
Công cụ và Máy Móc: Trong thiết kế máy móc và công cụ, tính diện tích toàn phần giúp đảm bảo rằng các bộ phận hình trụ có thể được chế tạo chính xác và lắp ráp hiệu quả.
Tính Toán Vật Liệu:
Tính Toán Vật Liệu Đóng Gói: Khi sản xuất bao bì, tính diện tích toàn phần của hình trụ giúp xác định lượng vật liệu đóng gói cần thiết.
Bảo Vệ và Sơn: Diện tích toàn phần giúp xác định số lượng sơn hoặc lớp phủ cần thiết để bảo vệ hoặc trang trí các bề mặt hình trụ.
Xây Dựng và Cơ Khí:
Cột và Trụ: Diện tích toàn phần của cột hoặc trụ trong các công trình xây dựng giúp xác định số lượng vật liệu cần thiết và phân phối tải trọng. Đây là yếu tố quan trọng trong thiết kế cầu, tòa nhà, và các công trình hạ tầng.
Ống và Bồn Chứa: Đối với các ống dẫn hoặc bồn chứa lớn, việc tính toán diện tích toàn phần giúp trong việc kiểm tra và đảm bảo khả năng chịu lực của các cấu trúc này.
Quản Lý và Bảo Trì:
Bảo Trì Định Kỳ: Diện tích toàn phần là cơ sở để đánh giá mức độ hao mòn của bề mặt hình trụ trong các thiết bị công nghiệp và hệ thống ống dẫn. Điều này giúp lập kế hoạch bảo trì và sửa chữa hiệu quả.
Phân Tích Chi Phí và Dự Toán:
Chi Phí Vật Liệu: Tính diện tích toàn phần giúp trong việc dự toán chi phí vật liệu cho các dự án xây dựng và sản xuất. Điều này giúp quản lý ngân sách và lập kế hoạch chi tiêu hiệu quả.
Chi Phí Sơn và Phủ Bề Mặt: Khi cần sơn hoặc phủ lớp bảo vệ cho các bề mặt hình trụ, diện tích toàn phần giúp tính toán chính xác lượng sơn hoặc lớp phủ cần thiết.
Tính Toán Hiệu Suất:
Hiệu Suất Của Các Hệ Thống: Trong một số ứng dụng công nghiệp, như hệ thống trao đổi nhiệt hoặc bình áp suất, diện tích toàn phần có thể ảnh hưởng đến hiệu suất hoạt động. Việc tính toán chính xác diện tích giúp tối ưu hóa hiệu suất và hiệu quả của các hệ thống này.
Định Hướng và Cài Đặt:
Lắp Đặt Thiết Bị: Trong việc lắp đặt thiết bị hình trụ như cột đèn, trụ điện, hoặc bồn chứa, diện tích toàn phần giúp đảm bảo các thiết bị được lắp đặt đúng cách và có đủ không gian.
Giáo Dục và Đào Tạo:
Học Tập Toán Học: Diện tích toàn phần của hình trụ là một phần quan trọng trong giáo dục toán học, giúp học sinh và sinh viên hiểu và áp dụng các công thức hình học trong các bài toán thực tế.
Diện tích toàn phần của hình trụ không chỉ là một khái niệm toán học cơ bản mà còn có nhiều ứng dụng thực tiễn quan trọng trong các lĩnh vực công nghiệp, thiết kế, quản lý và bảo trì.
Những bài tập về diện tích toàn phần hình trụ trong thực tế
Dưới đây là một số bài tập thực tế liên quan đến diện tích toàn phần của hình trụ, giúp bạn áp dụng lý thuyết vào các tình huống cụ thể:
Bài Tập 1: Tính Diện Tích Toàn Phần Của Chai Nước
Đề bài:
Một chai nước có hình dạng hình trụ với bán kính mặt đáy là 5 cm và chiều cao là 20 cm. Tính diện tích toàn phần của chai nước.
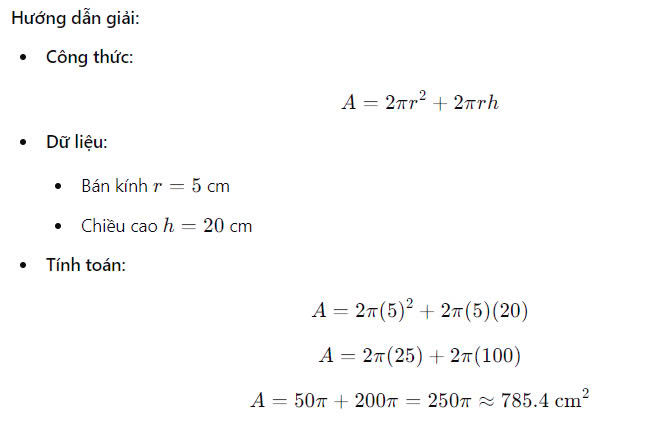
Bài tập 1
Bài Tập 2: Tính Diện Tích Toàn Phần Của Một Cột Cảnh Quan
Đề bài:
Một cột cảnh quan có hình dạng hình trụ với đường kính là 40 cm và chiều cao là 3 m. Tính diện tích toàn phần của cột.
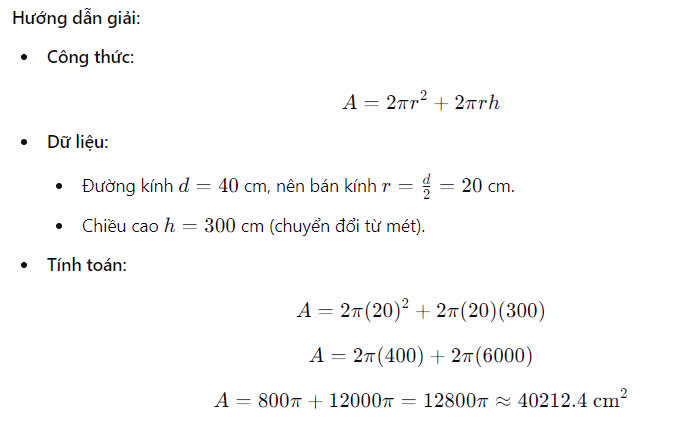
Bài tập 2
Bài Tập 3: Tính Diện Tích Toàn Phần Của Một Bồn Chứa Nước
Đề bài:
Một bồn chứa nước có hình dạng hình trụ với bán kính mặt đáy là 1,5 m và chiều cao là 2,5 m. Tính diện tích toàn phần của bồn chứa.

Bài tập 3
Bài Tập 4: Tính Diện Tích Toàn Phần Của Một Cây Cột Đèn
Đề bài:
Một cây cột đèn có hình dạng hình trụ với bán kính mặt đáy là 0,3 m và chiều cao là 7 m. Tính diện tích toàn phần của cột đèn.

Bài tập 4
Bài Tập 5: Tính Diện Tích Toàn Phần Của Một Bình Áp Suất
Đề bài:
Một bình áp suất hình trụ có đường kính là 80 cm và chiều cao là 1,2 m. Tính diện tích toàn phần của bình.

Bài tập 5
Những bài tập này giúp bạn áp dụng các công thức tính diện tích toàn phần của hình trụ vào các tình huống thực tế, từ các vật dụng hàng ngày đến các công trình và thiết bị công nghiệp.
Như vậy, chúng tôi đã chia sẻ cách tính diện tích xung quanh hình trụ và các kiến thức liên quan cho các bạn tham khảo. Mong rằng những thông tin trên giúp các bạn có thêm kiến thức, kỹ năng để giải các bài tập về hình trụ.
Để nhận được tư vấn về các dịch vụ do VINHOMES MIỀN BẮC cung cấp, vui lòng liên hệ qua Hotline: 0943.238.228 hoặc Email: duytran1185@gmail.com để nhận được tư vấn trực tiếp từ phía chuyên viên.
>> Tham khảo: Biệt thự song lập ocean park
Với nhiều năm kinh nghiệm trong lĩnh vực bất động sản, tôi TRẦN ĐỨC DUY - tự hào là một trong những chuyên gia tư vấn hàng đầu tại Việt Nam

































