Số Nguyên Tố Là Gì? Cách Kiểm Tra Số Có Phải Là Số Nguyên Tố Không?
Số nguyên tố là gì
Số nguyên tố là gì?
Số nguyên tố được định nghĩa là một số tự nhiên lớn hơn 1 và số nguyên tố chỉ có đúng hai ước số đó là: 1 và chính nó. Có nghĩa là số nguyên tố không thể chia hết cho bất kỳ số nào khác ngoài 1 và chính nó.
Ví dụ về số nguyên tố:
2; 3 ; 5 ; 7 ; 11 ; 13 ; 17 ; 19 ; 23 ; 29,...
Trong các số tự nhiên, 2 là số nguyên tố nhỏ nhất và cũng là số nguyên tố chẵn duy nhất, vì mọi số chẵn khác đều có thể chia hết cho số 2 nên số đó không phải là số nguyên tố. Các số lẻ còn lại đều là số nguyên tố.

Định nghĩa về số nguyên tố
Có bao nhiêu số nguyên tố?
Có vô hạn số nguyên tố. Điều này đã được chứng minh từ thời cổ đại bởi nhà toán học Hy Lạp Euclid. Trong chứng minh của ông, Euclid sử dụng phương pháp phản chứng để chỉ ra rằng không thể tồn tại một số lượng hữu hạn số nguyên tố.
Chứng minh cơ bản là: Nếu giả sử có một số lượng hữu hạn số nguyên tố, ta có thể tạo ra một số mới bằng cách nhân tất cả các số nguyên tố đó với nhau và cộng thêm 1. Số này không chia hết cho bất kỳ số nguyên tố nào trong danh sách, dẫn đến mâu thuẫn và chứng minh rằng số nguyên tố phải là vô hạn.
>> Xem thêm: Diện tích toàn phần hình trụ
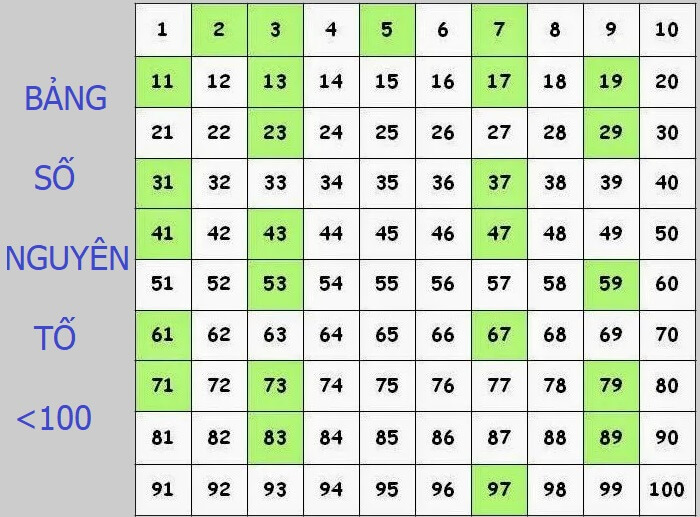
Có bao nhiêu số nguyên tố
Làm thế nào để kiểm tra một số có phải là số nguyên tố không?
Để kiểm tra một số có phải là số nguyên tố hay không, bạn có thể thực hiện theo các bước sau:
Kiểm tra các trường hợp đặc biệt:
- Nếu một số nhỏ hơn hoặc bằng 1, thì số đó không phải là số nguyên tố.
- Nếu số đó là 2, thì là số nguyên tố (2 là số nguyên tố chẵn duy nhất).
- Nếu một số là số chẵn mà lớn hơn 2, thì số đó không phải là số nguyên tố (vì mọi số chẵn lớn hơn 2 đều chia hết cho 2).
Thử chia số đó cho các số nguyên tố nhỏ hơn:
- Kiểm tra xem số đó có chia hết cho bất kỳ số nguyên tố nào nhỏ hơn căn bậc hai của số đó hay không. Nếu chia hết cho bất kỳ số nào trong khoảng này, thì không phải là số nguyên tố.
- Nếu không chia hết cho bất kỳ số nào trong khoảng này, thì số đó là số nguyên tố.
- Cụ thể hóa qua ví dụ:
- Giả sử ta muốn kiểm tra xem số 29 có phải là số nguyên tố hay không:
- Căn bậc hai của 29 là khoảng 5.39. Ta sẽ kiểm tra các số nguyên tố nhỏ hơn hoặc bằng 5, tức là: 2, 3, và 5.
- 29 không chia hết cho 2 (vì 29 là số lẻ).
- 29 không chia hết cho 3 (vì 29 chia 3 cho ra số lẻ là 9.67).
- 29 không chia hết cho 5 (vì tận cùng của 29 không phải là 0 hoặc 5).
- Vì 29 không chia hết cho bất kỳ số nào trong tập hợp các số nguyên tố nhỏ hơn hoặc bằng căn bậc hai của nó, nên 29 là một số nguyên tố.
- Thuật toán sàng Eratosthenes (Sieve of Eratosthenes):
Ngoài cách kiểm tra thủ công, nếu bạn cần tìm tất cả các số nguyên tố trong một phạm vi nhất định, bạn có thể sử dụng thuật toán sàng Eratosthenes. Thuật toán này loại bỏ các bội số của từng số nguyên tố trong một danh sách các số tự nhiên, giúp bạn nhanh chóng xác định các số nguyên tố trong phạm vi đó.

Vì sao số nguyên tố quan trọng
Tại sao số nguyên tố quan trọng?
Số nguyên tố là gì? Số nguyên tố quan trọng vì chúng đóng vai trò cơ bản và thiết yếu trong nhiều lĩnh vực của toán học và các ứng dụng thực tế. Dưới đây là những lý do tại sao số nguyên tố lại quan trọng:
Cơ sở của lý thuyết số:
Số nguyên tố được coi là "khối xây dựng" của các số tự nhiên. Theo định lý cơ bản của số học, mọi số nguyên lớn hơn 1 có thể phân tích duy nhất thành một tích của các số nguyên tố. Điều này giống như việc mọi hợp chất có thể được phân tích thành các nguyên tố hóa học, khiến số nguyên tố trở thành thành phần cơ bản nhất của số học.
Ứng dụng trong mật mã học (Cryptography):
Bảo mật dữ liệu: Các số nguyên tố đóng vai trò trung tâm trong các thuật toán mã hóa, đặc biệt là trong hệ thống mã hóa RSA. Các hệ thống bảo mật dữ liệu, như bảo mật giao dịch trực tuyến, truyền thông an toàn qua internet, sử dụng tính chất khó phân tích một số thành các thừa số nguyên tố lớn. Vì việc phân tích một số rất lớn thành các số nguyên tố là một bài toán cực kỳ khó khăn với các máy tính hiện đại, điều này giúp bảo vệ dữ liệu.
Lý thuyết toán học và nghiên cứu khoa học:
Lý thuyết số và các bài toán mở: Số nguyên tố kích thích nhiều nghiên cứu trong toán học, chẳng hạn như các bài toán về phân phối số nguyên tố, số nguyên tố sinh đôi, số nguyên tố Mersenne và các câu hỏi về số nguyên tố chưa được giải quyết. Những nghiên cứu này có thể dẫn đến những phát minh mới trong toán học và các lĩnh vực liên quan.
Ứng dụng trong thuật toán và khoa học máy tính:
Thuật toán tối ưu hóa: Số nguyên tố được sử dụng trong các thuật toán để tìm kiếm các số nguyên tố lớn, giúp tăng tốc độ xử lý trong các ứng dụng về mật mã, số học tính toán và các hệ thống phân tán.
Sinh số ngẫu nhiên: Một số thuật toán sinh số ngẫu nhiên trong khoa học máy tính dựa trên các tính chất của số nguyên tố.
Ứng dụng trong lý thuyết mã hóa và truyền thông:
Phát hiện và sửa lỗi: Số nguyên tố được sử dụng trong lý thuyết mã hóa và truyền thông để phát hiện và sửa lỗi trong các hệ thống truyền tin, chẳng hạn như mã Hamming và các mã phát hiện lỗi khác.
Ứng dụng trong vật lý và thiên văn học:
Mô hình hóa tự nhiên: Một số hiện tượng tự nhiên và các hệ thống vật lý có thể được mô hình hóa bằng các nguyên lý liên quan đến số nguyên tố. Các mô hình này có thể giúp giải thích cấu trúc của một số đối tượng hoặc hiện tượng, từ cấu trúc phân tử đến sự phân phối của các thiên thể.
Định lý toán học quan trọng:
Các định lý quan trọng trong toán học, như định lý nhỏ Fermat, định lý Euler hay định lý số nguyên tố, đều liên quan mật thiết đến số nguyên tố, giúp cung cấp cơ sở cho nhiều công trình nghiên cứu trong toán học lý thuyết và ứng dụng.
Tóm lại:
Số nguyên tố là gì? Số nguyên tố có ý nghĩa cơ bản trong việc xây dựng số học, ứng dụng mạnh mẽ trong bảo mật thông tin và mật mã học, cùng với vai trò quan trọng trong nghiên cứu toán học và khoa học. Chúng là những khối xây dựng không thể thiếu trong nhiều lĩnh vực khác nhau của toán học và công nghệ hiện đại.
Trên đây là những thông tin giúp bạn biết số nguyên tố là gì, các tính chất và khái niệm liên quan đến số nguyên tố. Hi vọng đây sẽ là các kiến thức hữu ích mà bạn có thể tích lũy và vận dụng trong việc tính toán cũng như nhiều khía cạnh khác trong cuộc sống.
Để nhận được tư vấn về các dịch vụ do VINHOMES MIỀN BẮC cung cấp, vui lòng liên hệ qua Hotline: 0943.238.228 hoặc Email: duytran1185@gmail.com để nhận được tư vấn trực tiếp từ phía chuyên viên.
>> Tham khảo: Biệt thự liền kề vinhomes ocean park
Với nhiều năm kinh nghiệm trong lĩnh vực bất động sản, tôi TRẦN ĐỨC DUY - tự hào là một trong những chuyên gia tư vấn hàng đầu tại Việt Nam