Kiến Thức Hữu Ích
Công thức tính diện tích toàn phần hình trụ đầy đủ, dễ hiểu
1/15/2026 6:04:00 PM
5/5 - (0
Bình chọn )
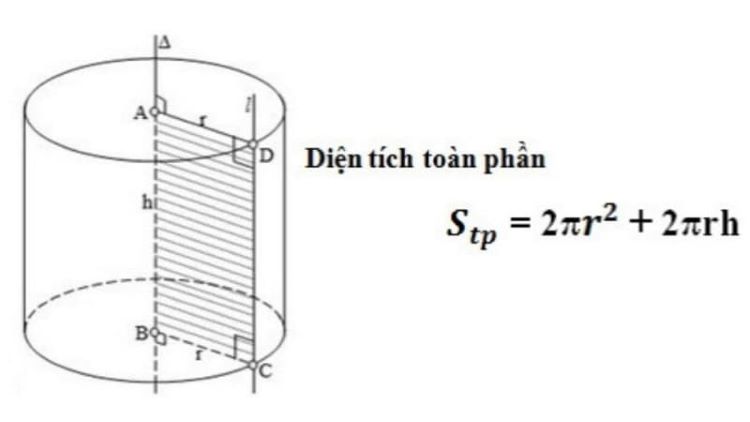
Diện tích toàn phần hình trụ
1.Diện tích toàn phần hình trụ là gì?
Diện tích toàn phần của hình trụ là tổng diện tích của hai đáy hình tròn và diện tích xung quanh hình trụ. Nói cách khác, đây là toàn bộ bề mặt ngoài của hình trụ, bao gồm cả phần đáy trên, đáy dưới và phần bên quanh trụ.
Cụ thể:
Đáy hình trụ là hai hình tròn giống hệt nhau, mỗi đáy có diện tích S_đáy = π × r² (r là bán kính đáy).
Diện tích xung quanh là hình chữ nhật khi “mở” phần bên của hình trụ ra, có diện tích S_xq = 2 × π × r × h (h là chiều cao trụ).
2.Công thức tính diện tích toàn phần hình trụ như thế nào?
Công thức:
S_toan_phan = 2 × π × r × h + 2 × π × r²
Trong đó:
r : bán kính đáy hình trụ
h : chiều cao hình trụ
π : hằng số Pi (~3,1416)
S_toan_phan : diện tích toàn phần của hình trụ
Rút gọn:
S_toan_phan = 2 × π × r × (r + h)
Công thức này vừa bao gồm diện tích xung quanh (2 × π × r × h) vừa cộng diện tích hai đáy (2 × π × r²), giúp tính tổng bề mặt ngoài của hình trụ.
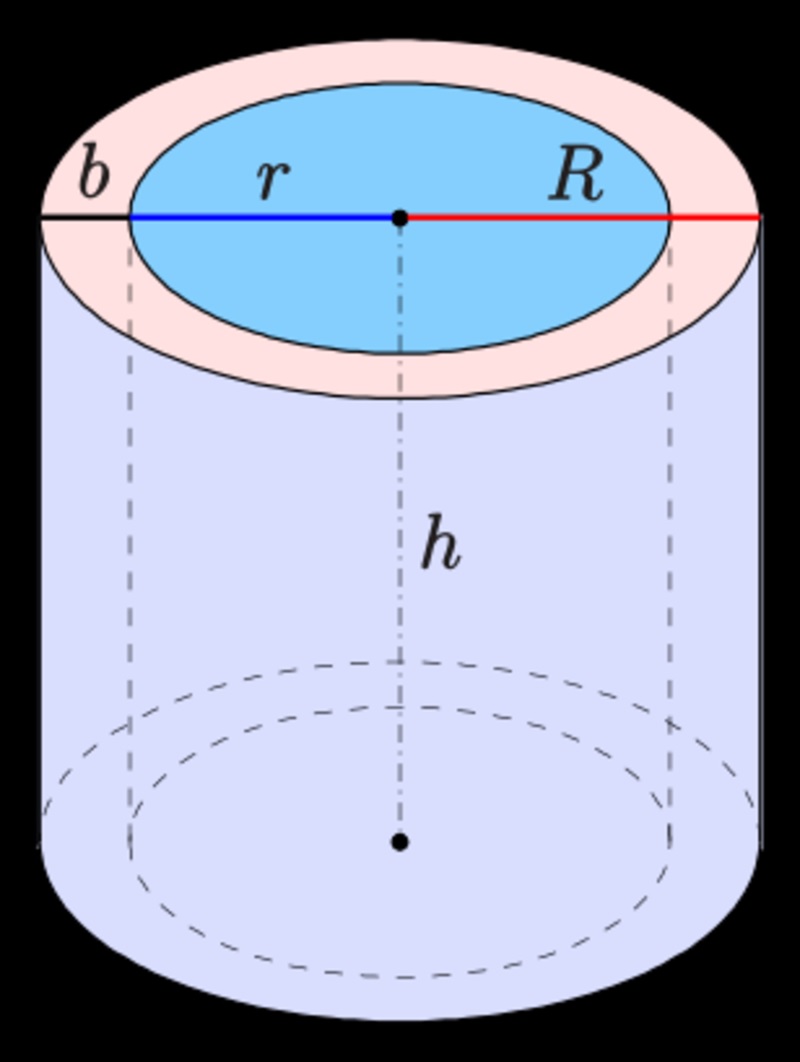
Công thức tính diện tích xung quanh của hình trụ
3.Cách tính diện tích xung quanh và diện tích toàn phần hình trụ
Dưới đây là hướng dẫn cách tính diện tích xung quanh và diện tích toàn phần của hình trụ một cách rõ ràng, dễ hiểu và dễ áp dụng:
Diện tích xung quanh hình trụ (S_xq)
Diện tích xung quanh là diện tích của mặt bên hình trụ khi bạn “mở” nó ra sẽ thành một hình chữ nhật có:
Chiều dài = chu vi đáy = 2 × π × r
Chiều cao = h
Công thức:
S_xq = 2 × π × r × h
Trong đó:
r : bán kính đáy hình trụ
h : chiều cao hình trụ
π : hằng số Pi (~3,1416)
📌 Ví dụ: Hình trụ có bán kính r = 3 cm, chiều cao h = 5 cm
S_xq = 2 × π × 3 × 5 = 30π cm²
2. Diện tích toàn phần của hình trụ (S_tp)
Diện tích toàn phần là tổng diện tích xung quanh và diện tích hai đáy tròn:
S_toan_phan = S_xq + 2 × S_day
Công thức cụ thể:
S_toan_phan = 2 × π × r × h + 2 × π × r²
Hoặc rút gọn:
S_toan_phan = 2 × π × r × (r + h)
📌 Ví dụ: Hình trụ có bán kính r = 3 cm, chiều cao h = 5 cm
S_toan_phan = 2 × π × 3 × (3 + 5) = 48π cm²
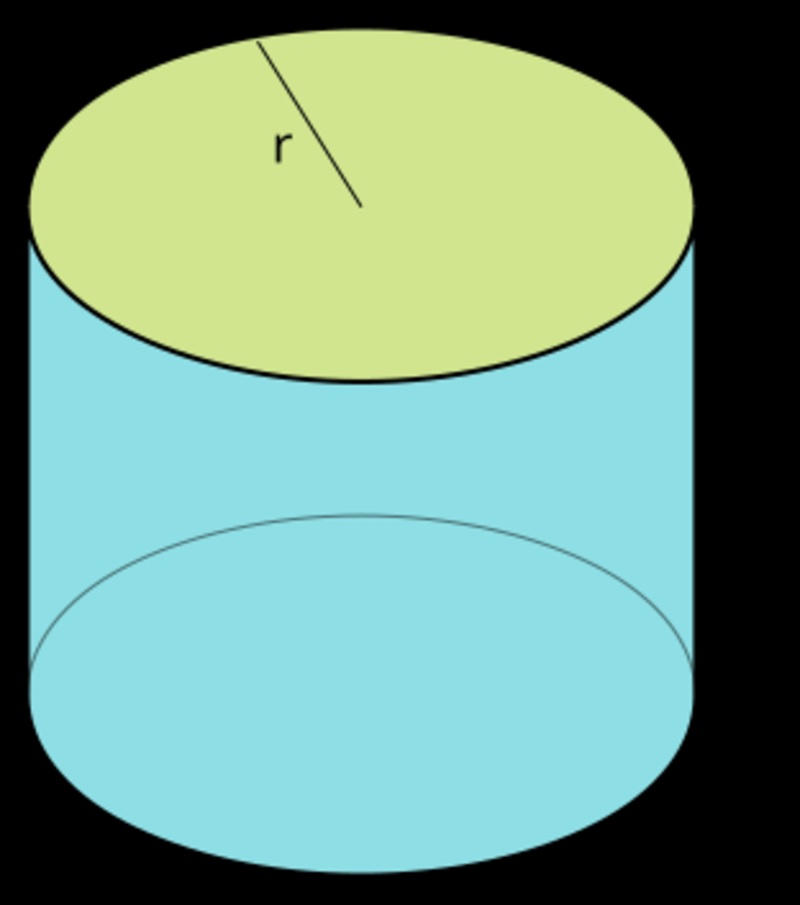
Cách tính diện tích xung quanh
4.Bài tập về diện tích toàn phần của hình trụ có lời giải chi tiết
Dưới đây là một số bài tập về diện tích toàn phần của hình trụ kèm lời giải chi tiết, giúp bạn luyện tập và hiểu rõ cách áp dụng công thức:
Bài tập 1
Hình trụ có bán kính đáy r = 4 cm và chiều cao h = 10 cm. Tính:
a) Diện tích xung quanh
b) Diện tích toàn phần
Lời giải:
a) Diện tích xung quanh:
S_xq = 2 × π × r × h
= 2 × π × 4 × 10
= 80π cm²
b) Diện tích toàn phần:
S_toan_phan = 2 × π × r × (r + h)
= 2 × π × 4 × (4 + 10)
= 2 × π × 4 × 14
= 112π cm²
Bài tập 2
Hình trụ có bán kính đáy r = 3 cm và chiều cao h = 5 cm. Tính diện tích xung quanh và diện tích toàn phần.
Lời giải:
Diện tích xung quanh:
S_xq = 2 × π × r × h
= 2 × π × 3 × 5
= 30π cm²
Diện tích toàn phần:
S_toan_phan = 2 × π × r × (r + h)
= 2 × π × 3 × (3 + 5)
= 48π cm²
Bài tập 3
Một hình trụ có diện tích xung quanh S_xq = 94,2 cm² và bán kính đáy r = 3 cm. Tính chiều cao h và diện tích toàn phần.
Lời giải:
Tính chiều cao:
S_xq = 2 × π × r × h
94,2 = 2 × 3,14 × 3 × h
94,2 = 18,84 × h
h = 94,2 / 18,84
h ≈ 5 cm
Tính diện tích toàn phần:
S_toan_phan = 2 × π × r × (r + h)
= 2 × 3,14 × 3 × (3 + 5)
= 6,28 × 3 × 8
= 150,72 cm²
Bài tập 4
(Thử thách)
Hình trụ có diện tích toàn phần S_tp = 226,08 cm² và bán kính đáy r = 6 cm. Tính chiều cao h.
Lời giải:
S_toan_phan = 2 × π × r × (r + h)
226,08 = 2 × 3,14 × 6 × (6 + h)
226,08 = 37,68 × (6 + h)
6 + h = 226,08 / 37,68
6 + h ≈ 6
h ≈ 0 cm
→ Trường hợp này nghĩa là hình trụ rất thấp (gần như chỉ là hai đáy).

Ứng dụng của diện tích xung quanh của hình trụ
5.Mẹo học thuộc công thức diện tích toàn phần hình trụ nhanh chóng
Dưới đây là một số mẹo học thuộc công thức diện tích toàn phần của hình trụ nhanh chóng, dễ nhớ và áp dụng được ngay:
Nhớ theo cấu trúc “xung quanh + hai đáy”
Công thức diện tích toàn phần là:
S_toan_phan = S_xq + 2 × S_day
S_xq là diện tích xung quanh
S_day là diện tích mỗi đáy hình tròn
Việc chia nhỏ công thức thành hai phần giúp não dễ ghi nhớ hơn.
Sử dụng công thức rút gọn
S_toan_phan = 2 × π × r × (r + h)
Học theo công thức rút gọn dễ nhớ hơn so với ghi từng phần riêng lẻ.
Có thể tưởng tượng hình trụ như một lon nước: 2 đáy + xung quanh.
Hình dung hình trụ và “mở” thành hình chữ nhật
Khi mở mặt xung quanh hình trụ ra, bạn sẽ thấy một hình chữ nhật có chiều dài = chu vi đáy (2 × π × r) và chiều cao = h.
Học theo hình ảnh trực quan giúp não ghi nhớ công thức nhanh hơn.
Dùng câu nhẩm hoặc công thức vần điệu
Ví dụ:
“Diện tích toàn phần = 2πr × (r + h)”
2 đáy cộng xung quanh, r và h nhớ liền nhau.”
Những câu nhẩm vui nhộn hoặc vần điệu giúp học thuộc lâu hơn.
Luyện tập nhiều bài tập
Làm nhiều ví dụ thực tế, từ bài đơn giản đến phức tạp.
Việc áp dụng công thức nhiều lần giúp não ghi nhớ tự động, không phải học thuộc máy móc.
📌 Kết luận:
Nhớ công thức theo cấu trúc 2 phần, hình dung trực quan và luyện tập thường xuyên là cách nhanh nhất để học thuộc công thức diện tích toàn phần của hình trụ một cách bền vững và chính xác.
Trên đây, chúng tôi đã tổng hợp và trình bày đầy đủ các kiến thức về diện tích toàn phần của hình trụ, bao gồm định nghĩa, công thức, cách tính diện tích xung quanh, bài tập minh họa và mẹo học thuộc nhanh chóng. Hy vọng bài viết sẽ giúp bạn nắm vững kiến thức, áp dụng chính xác công thức và tự tin giải các bài toán liên quan đến hình trụ trong học tập cũng như thực tế.