Bất Đẳng Thức Bunhiacopxki: Lý Thuyết, Công Thức, Cách Áp Dụng
Bất đẳng thức Bunhiacopxki là gì?
Bất đẳng thức Bunhiacopxki có tên chính xác là bất đẳng thức Cauchy – Bunhiacopxki – Schwarz. Sau đó được rút gọn lại theo tên của nhà toán học người Nga Bunhiacopxki. Bất đẳng thức này thực chất do 3 nhà toán học nghiên cứu và phát triển. Trong lĩnh vực toán học, bất đẳng thức này có nhiều ứng dụng để giải các bài toán chứng minh bất đẳng thức và tìm cực trị.
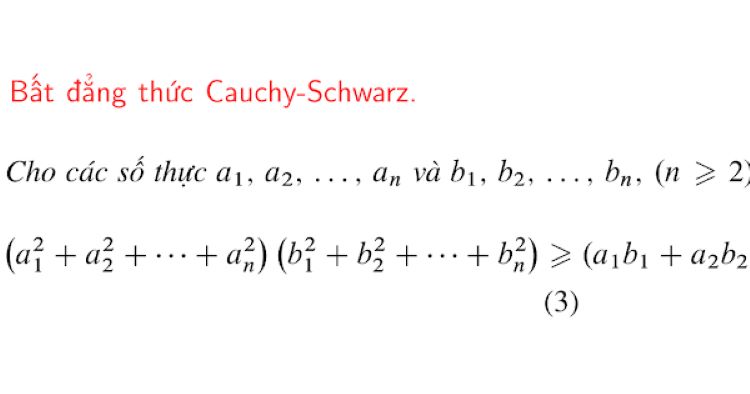
BĐT Bunhiacopxki
Công thức Bất đẳng thức Bunhiacopxki
Bất đẳng thức Bunhiacopxki dạng cơ bản
(a²+b²) (c²+d²) ≥(ac+bd)²
Dấu "=" xảy ra khi ac=bd
Bất đẳng thức Cauchy-Schwarz dạng tổng quát
Với hai bộ số (a₁, a₂,..., aₙ) và (b₁, b₂, ..., bₙ), ta có:
(a₁² + a₂² +...+ aₙ²). (b₁² + b₂² +... + bₙ²)≥ (a₁b₁+a₂b₂+...+aₙbₙ)²
Dấu "=" xảy ra khi a₁/b₁=a₂/b₂=...=aₙ/bₙ
Nếu một số nào đó (i=1,2,3,...,n) bằng 0 thì đẳng thức tương ứng bằng 0.
Bất đẳng thức Cauchy-Schwarz
Theo dõi chi tiết ở bảng sau:

Bất đẳng thức Cauchy-Schwarz
Hệ quả của bất đẳng thức Cauchy-Schwarz
Hệ quả 1
Nếu a₁x₁+...+aₙxₙ= C thì min (x₁² +...+xₙ² )= c/(a₁² +...+ aₙ² ) đạt được khi x₁/a₁=...= xₙ/aₙ
Hệ quả 2
Nếu x₁² +...+ xₙ² = C² ( không đổi) thì:
Max (a₁x₁+...+aₙxₙ)= c√( a₁² +...+ aₙ² )đạt được khi a₁x₁=....=aₙx≥ 0
Min (a₁x₁+...+aₙxₙ) = -c√( a₁² +...+ aₙ² ) và dấu "=" xảy ra khi a₁x₁=....=aₙx≤ 0
Chứng minh bất đẳng thức Cauchy-Schwarz
Chúng ta có thể chứng minh bất đẳng thức Bunhiacopxki bằng cách:
(a²+b²)(c²+d²)≥(ac+bd)²
⇔ (ac)² +(ad)² +(bc)²+ (bd)² ≥(ac)²+ 2acbcd+(bd)²
⇔ (ad)² + (bc)² ≥ 2abcd
⇔ (ad)² - 2abcd + (bc)²≥0
⇔ (ad-bc)² ≥0 (luôn đúng)
>> Tham khảo: Bảng nguyên tố hóa học
Ứng Dụng Của bất đẳng thức Cauchy-Schwarz
Bất đẳng thức Cauchy-Schwarz là 1 trong số những dạng bất đẳng thức quan trọng trong toán học. Bất đẳng thức này được ứng dụng trong nhiều bài toán về hình học, đại số và các vấn đề bất đẳng thức khác. Dưới đây là một số ứng dụng quan trọng của bất đẳng thức này:
Giải bài toán bất đẳng thức phân thức: Bunhiacopxki được dùng để chứng minh nhiều bất đẳng thức chứa các đại lượng dạng phân thức. Nhất là trong các bài toán tìm giá trị lớn nhất hoặc nhỏ nhất của một biểu thức.
Ứng dụng trong hình học: Bất đẳng thức Cauchy-Schwarz giúp giải quyết nhiều bài toán hình học. Bao gồm việc chứng minh các bất đẳng thức liên quan đến tam giác hoặc tứ giác, hay các bài toán về đường tròn và đường thẳng.
Tìm giá trị cực đại, cực tiểu: Bất đẳng thức này được ứng dụng để tìm giá trị lớn nhất(max) hoặc nhỏ nhất (min) của một hàm số hoặc một biểu thức phức tạp. Một trong những kỹ thuật phổ biến chính là áp dụng bất đẳng thức để đánh giá tổng hoặc tích của các biến.
Kỹ thuật thêm bớt và đổi biến: Trong 1 số trường hợp, việc sử dụng kỹ thuật thêm bớt các biến phù hợp hoặc thực hiện các phép đổi biến. Điều này có thể giúp ta dễ dàng áp dụng BĐT Bunhiacopxki để giải quyết các bài toán phức tạp hơn.
Chứng minh các bất đẳng thức khác Nhiều bất đẳng thức nổi tiếng trong toán học có thể được chứng minh một cách đơn giản bằng cách dùng Bunhiacopxki. Ví dụ, việc chứng minh các bất đẳng thức dạng có
1/a +1/b+ 1/c ≥9 khi a+b +c = 1
Nhờ vào tính tổng quát và linh hoạt, bất đẳng thức Cauchy-Schwarz không chỉ xuất hiện trong các bài toán lý thuyết. Mà còn là công cụ mạnh mẽ được dùng trong các bài toán thực tiễn và các lĩnh vực toán học khác.
Bài tập ứng dụng bất đẳng thức Cauchy-Schwarz
Bài 1: Cho a, b, c là các số thực dương bất kỳ. Chứng minh rằng:
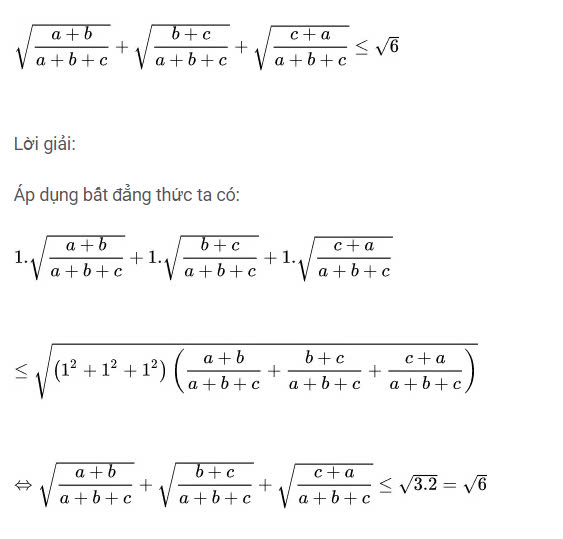
Dấu “=” xảy ra khi và chỉ khi giá trị a = b = c
Bài 2: Tìm giá trị lớn nhất của biểu thức dưới đây:
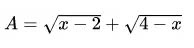
Lời giải:
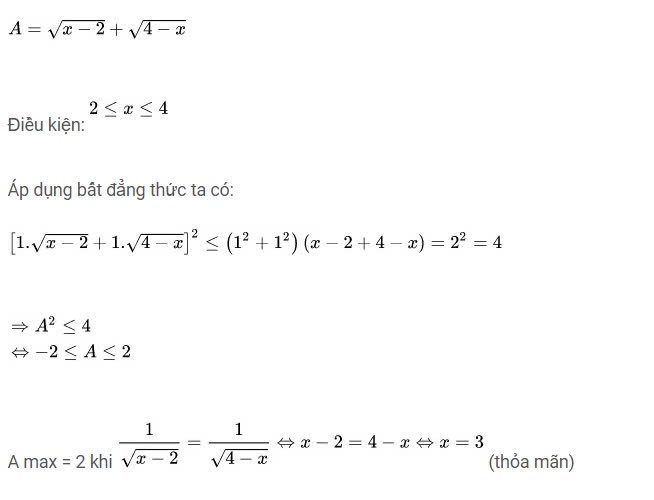
Vậy max A = 2 khi và chỉ khi giá trị x = 3
>> Tham khảo: Bán chung cư vinhome ocean park
Với nhiều năm kinh nghiệm trong lĩnh vực bất động sản, tôi TRẦN ĐỨC DUY - tự hào là một trong những chuyên gia tư vấn hàng đầu tại Việt Nam