Bất Đẳng Thức Bunhiacopxki Là Gì? Lý Thuyết, Cách Chứng Minh

Khái niệm và phát biểu bất đẳng thức Bunhiacopxki

Bất đẳng thức Bunhiacopxki (hay còn gọi là Cauchy-Schwarz) là một dạng bất đẳng thức kinh điển trong toán học, liên quan đến tổng và tích của hai dãy số thực.

Phát biểu tổng quát của bất đẳng thức :

Cho hai dãy số thực a₁, a₂, ..., aₙ và b₁, b₂, ..., bₙ, ta có:

(a₁² + a₂² + ... + aₙ²) × (b₁² + b₂² + ... + bₙ²) ≥ (a₁b₁ + a₂b₂ + ... + aₙbₙ)²

Hay viết ngắn gọn bằng ký hiệu tổng:

(Σ aᵢ²) × (Σ bᵢ²) ≥ (Σ aᵢbᵢ)², với i chạy từ 1 đến n

Dấu "=" xảy ra khi nào?

Dấu bằng xảy ra khi và chỉ khi tồn tại một số thực k sao cho với mọi i, ta có: aᵢ = k × bᵢ (tức là hai dãy tỉ lệ với nhau).

Bất đẳng thức

Chứng minh bất đẳng thức

Ta sẽ chứng minh bất đẳng thức theo một cách phổ biến bằng cách sử dụng biểu thức bình phương không âm.

Cách chứng minh:

Xét biểu thức sau:

P(x) = (a₁x + b₁)² + (a₂x + b₂)² + ... + (aₙx + bₙ)²

Rõ ràng, P(x) ≥ 0 với mọi x ∈ ℝ vì là tổng các bình phương.

Mở rộng biểu thức:

P(x) = x²(a₁² + a₂² + ... + aₙ²) + 2x(a₁b₁ + a₂b₂ + ... + aₙbₙ) + (b₁² + b₂² + ... + bₙ²)

Gọi:

A = Σ aᵢ²

B = Σ bᵢ²

C = Σ aᵢbᵢ

=> P(x) = Ax² + 2Cx + B

Vì P(x) ≥ 0 ∀ x ⇒ phương trình bậc hai Ax² + 2Cx + B không có nghiệm thực, hay:

Δ = (2C)² - 4AB ≤ 0 ⇒ 4C² ≤ 4AB ⇒ C² ≤ AB

Tức là:

(Σ aᵢbᵢ)² ≤ (Σ aᵢ²) × (Σ bᵢ²)

Vậy ta có điều phải chứng minh.

Học sinh trong giờ toán

Ứng dụng của bất đẳng thức

Bất đẳng thức không chỉ là một kết quả lý thuyết mà còn có rất nhiều ứng dụng trong thực hành toán học và cả trong các lĩnh vực khác.

Trong giải toán bất đẳng thức

Được dùng để so sánh hai biểu thức chứa tổng và tích.

Là công cụ mạnh trong các bài toán cần tìm min – max của biểu thức.

Được dùng kết hợp với các bất đẳng thức khác như Cauchy, AM-GM, Holder...

Ví dụ:

Chứng minh rằng với mọi số thực x, y, ta có:

(x² + y²)(1 + 1) ≥ (x + y)²

Giải:

Áp dụng Bunhiacopxki với a₁ = x, a₂ = y; b₁ = 1, b₂ = 1

(x² + y²)(1² + 1²) = (x² + y²)(2) ≥ (x + y)²

⇒ Đpcm

Trong hình học

Giúp chứng minh các bất đẳng thức trong tam giác, tứ giác, hình không gian.

Là cơ sở để chứng minh các định lý về khoảng cách, góc giữa hai vector.

Ví dụ trong không gian vector:

Cho hai vector a và b trong không gian Euclid, ta có:

|a·b| ≤ ||a|| × ||b||

Đây chính là phiên bản hình học của bất đẳng thức Bunhiacopxki.

Trong vật lý và khoa học

Ứng dụng trong lý thuyết sóng, lượng tử và thống kê.

Dùng trong xử lý tín hiệu, học máy (machine learning), đặc biệt khi tính cosine similarity giữa các vector.

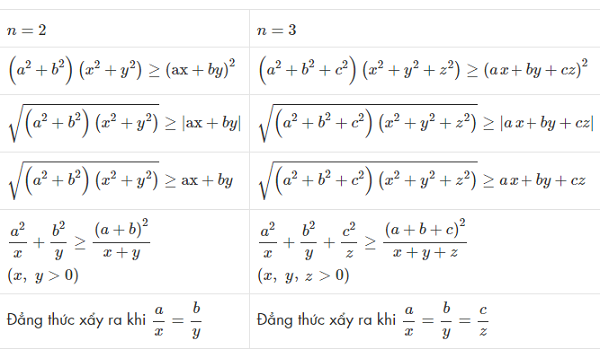
Minh họa trực quan bất đẳng thức Bunhiacopxki

Mẹo học và ghi nhớ bất đẳng thức Bunhiacopxki

Việc ghi nhớ và áp dụng bất đẳng thức sẽ dễ dàng hơn nếu bạn hiểu bản chất và luyện tập đúng cách.

Hiểu bản chất thay vì học thuộc

Bản chất của bất đẳng thức là "tổng của tích bình phương ≥ bình phương của tổng tích".

Có thể nhớ bằng cụm từ: “Tổng bình phương × Tổng bình phương ≥ Bình phương tổng tích”

So sánh với các bất đẳng thức quen thuộc

Bunhiacopxki thường đi kèm với bất đẳng thức Cauchy hoặc AM-GM.

Nhận diện bài toán khi có tổng các bình phương và tích các phần tử → nghĩ ngay đến Bunhiacopxki.

Học qua ví dụ cụ thể

Thay vì chỉ đọc lý thuyết, hãy làm thật nhiều ví dụ từ dễ đến khó. Một số đề thi học sinh giỏi, Olympic toán học có rất nhiều bài sử dụng Bunhiacopxki.

Ví dụ học sinh giỏi:

Chứng minh:

(a² + b² + c²)(x² + y² + z²) ≥ (ax + by + cz)²

Lời giải:

Áp dụng Bunhiacopxki trực tiếp cho 2 dãy a, b, c và x, y, z → Đpcm

Ghi nhớ trường hợp dấu “=” xảy ra

Đây là điểm dễ bị bỏ qua trong bài thi. Để đạt điểm tuyệt đối, bạn cần nhớ:

Dấu “=” xảy ra khi: tồn tại số k sao cho aᵢ = k × bᵢ ∀ i

Bất đẳng thức Bunhiacopxki là một công cụ toán học mạnh mẽ, đơn giản nhưng có giá trị ứng dụng cao. Việc nắm vững cách sử dụng và áp dụng đúng lúc sẽ giúp bạn giải quyết hiệu quả các bài toán bất đẳng thức, hình học cũng như các bài toán trong khoa học kỹ thuật.

Hãy bắt đầu bằng việc hiểu bản chất, luyện tập qua ví dụ cụ thể và không ngừng rèn luyện. Chỉ khi đó, bất đẳng thức Bunhiacopxki mới trở thành "vũ khí lợi hại" trong hành trang chinh phục Toán học của bạn.