Bất Đẳng Thức Bunhiacopxki Là Gì? Cách Hiểu, Áp Dụng Và Ví Dụ Dễ Nhớ

Tìm hiểu bất đẳng thức Bunhiacopxki là gì, cách ghi nhớ và vận dụng vào các bài toán thực tế. Hướng dẫn đơn giản, dễ hiểu, phù hợp cho học sinh và người luyện thi.

1. Bất đẳng thức Bunhiacopxki là gì và xuất phát từ đâu?

Nguồn gốc và tên gọi đặc biệt

Bất đẳng thức Bunhiacopxki là một trong những bất đẳng thức nổi tiếng trong đại số và giải tích, được đặt theo tên của nhà toán học người Nga – Viktor Yakovlevich Bunyakovsky. Trong một số tài liệu tiếng Pháp hoặc tiếng Anh, bạn có thể thấy nó còn được gọi là bất đẳng thức Cauchy – Schwarz hoặc Cauchy – Bunyakovsky – Schwarz.

Tên gọi này xuất phát từ việc cùng lúc ba nhà toán học, ở các thời điểm và vùng địa lý khác nhau, đã phát hiện ra những biểu thức tương đương của bất đẳng thức này. Dù xuất hiện từ thế kỷ 19, bất đẳng thức vẫn giữ nguyên giá trị cho đến nay, trở thành công cụ cực kỳ mạnh mẽ trong việc giải các bài toán từ cấp cơ bản đến nâng cao.

Ý nghĩa trong toán học

Bản chất của bất đẳng thức Bunhiacopxki là so sánh tích của tổng hai bình phương với bình phương của tổng tích tương ứng. Đây là bất đẳng thức thể hiện mối liên hệ giữa hai dãy số hoặc hai vectơ, và thường được áp dụng trong không gian Euclid, giải tích tổ hợp, hình học và nhiều dạng bài thi học sinh giỏi.

Ngoài ra, bất đẳng thức này còn là công cụ đánh giá cực trị, đặc biệt trong các bài toán chứng minh, tối ưu hóa hoặc tìm giá trị lớn nhất, nhỏ nhất. Việc nắm vững và hiểu rõ cách áp dụng bất đẳng thức này giúp bạn giải quyết rất nhiều bài toán phức tạp một cách hiệu quả.

Biểu thức toán học của bất đẳng thức trong trường hợp đại số

2. Biểu thức tổng quát của bất đẳng thức

Dạng đại số cơ bản

Trong trường hợp đơn giản nhất với hai dãy số thực a1,a2,...,ana_1, a_2, ..., a_n và b1,b2,...,bnb_1, b_2, ..., b_n, bất đẳng thức được viết như sau:

(a₁² + a₂² + ... + aₙ²)(b₁² + b₂² + ... + bₙ²) ≥ (a₁b₁ + a₂b₂ + ... + aₙbₙ)²

Biểu thức này cho biết rằng tích của tổng bình phương hai dãy số luôn lớn hơn hoặc bằng bình phương tổng tích các cặp số tương ứng. Dấu “=” xảy ra khi và chỉ khi tồn tại một hằng số k sao cho aᵢ = k * bᵢ với mọi i.

Ví dụ với hai dãy số ngắn như a = (1, 2) và b = (3, 4), bạn có thể dễ dàng kiểm tra bằng cách thay trực tiếp vào công thức. Tổng bình phương từng dãy, sau đó nhân lại, luôn lớn hơn hoặc bằng bình phương tổng tích từng cặp tương ứng.

Dạng tích phân trong giải tích

Trong giải tích, bất đẳng thức còn có một biểu thức tích phân như sau:

∫[a→b] f(x)² dx * ∫[a→b] g(x)² dx ≥ [∫[a→b] f(x)g(x) dx]²

Đây là dạng mở rộng cho hàm số liên tục trong đoạn [a, b]. Từ dạng này, người ta ứng dụng vào phân tích hàm số, xác định giới hạn, chứng minh hội tụ, hoặc nghiên cứu phương trình vi phân.

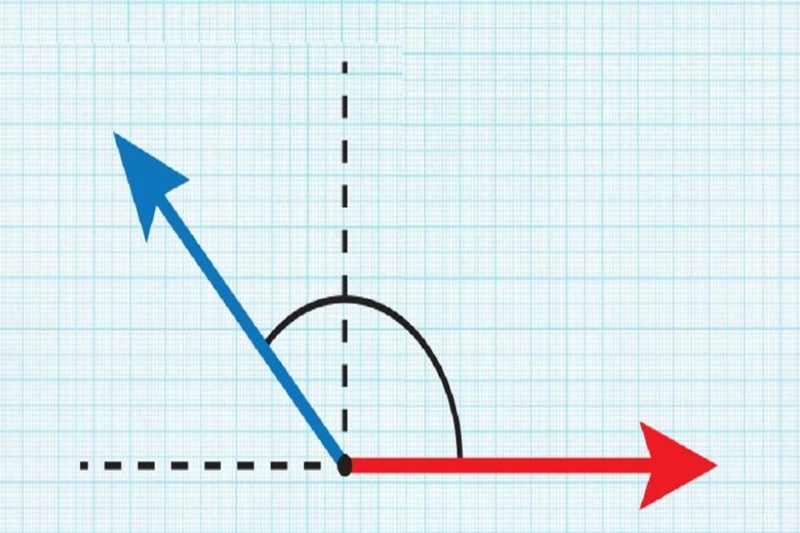
Minh họa độ dài hai vectơ và góc giữa chúng qua bất đẳng thức

3. Cách ghi nhớ và áp dụng bất đẳng thức Bunhiacopxki

Cách ghi nhớ đơn giản bằng hình ảnh

Một cách học nhanh bất đẳng thức là liên hệ với dạng tổng quát của hằng đẳng thức đáng nhớ:

(a² + b²)(x² + y²) ≥ (ax + by)²

Bạn có thể liên tưởng điều này giống như việc “phân phối năng lượng” từ hai vế khác nhau. Tổng bình phương hai vế tạo nên một “cái khung” rộng hơn so với phần giao nhau nằm giữa. Điều đó giúp hình dung rõ ràng rằng tích hai bình phương bao giờ cũng tạo ra diện tích lớn hơn so với một phần tử ghép đôi từ hai dãy.

Cách ghi nhớ tốt là luôn nghĩ đến việc: hai tổng bình phương sẽ luôn lớn hơn bình phương của tổng tích riêng lẻ – trừ khi các số “cùng hướng” hoặc tỉ lệ với nhau, khi đó hai vế mới bằng nhau.

Những trường hợp điển hình thường gặp

Trong các đề thi học sinh giỏi hoặc kỳ thi vào lớp 10, đại học, bạn thường bắt gặp dạng bài yêu cầu chứng minh một biểu thức lớn hơn hoặc bằng một giá trị cụ thể. Khi nhìn thấy tổng các bình phương, hoặc tổng có tích lặp lại giữa hai dãy, bạn có thể nghĩ đến việc áp dụng bất đẳng thức Bunhiacopxki.

Ví dụ, chứng minh:

(x + y + z)² ≤ 3(x² + y² + z²)

Bằng cách đặt a = (1, 1, 1) và b = (x, y, z), áp dụng bất đẳng thức ta có:

(1² + 1² + 1²)(x² + y² + z²) ≥ (x + y + z)²

Tức là: 3(x² + y² + z²) ≥ (x + y + z)²

Suy ra điều phải chứng minh.

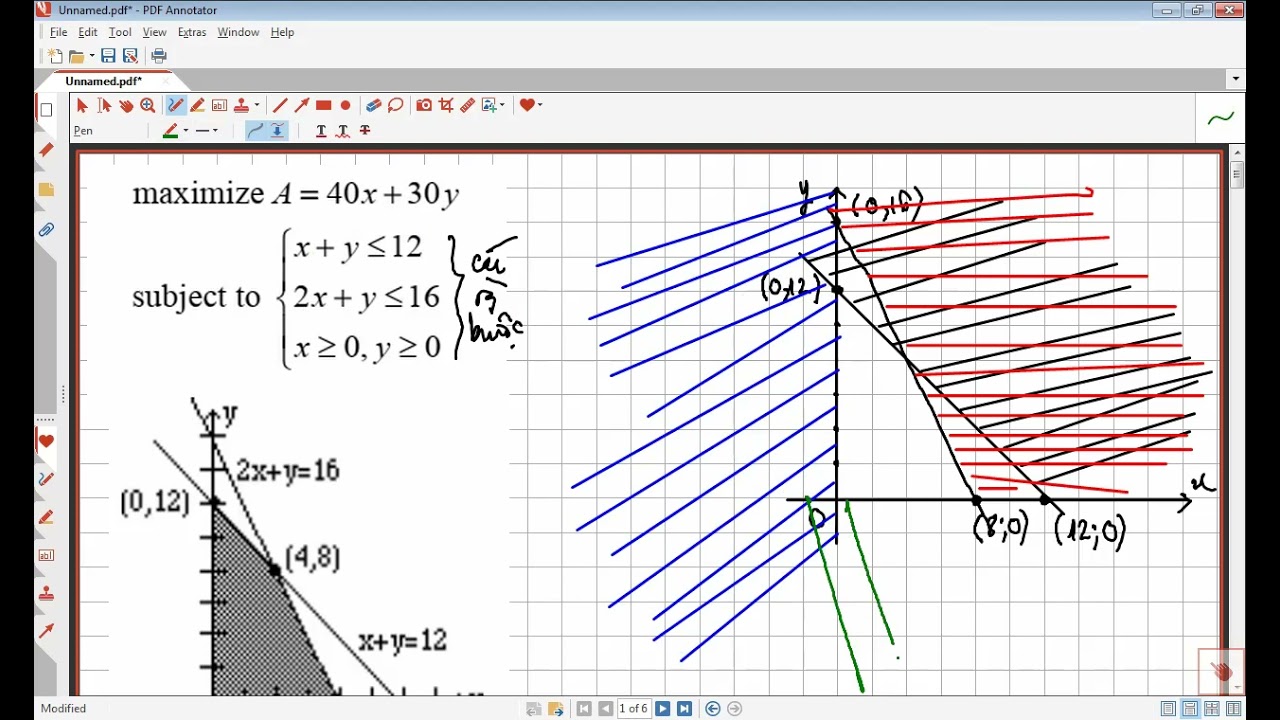
Áp dụng bất đẳng thức trong bài toán tối ưu hóa

4. Ý nghĩa mở rộng và ứng dụng thực tế của bất đẳng thức 

Trong không gian vector và hình học

Bất đẳng thức có vai trò cực kỳ quan trọng trong hình học không gian và đại số tuyến tính. Trong không gian Euclid, đây là cơ sở để chứng minh định nghĩa góc giữa hai vectơ. Nếu bạn có hai vectơ A và B, thì biểu thức:

|A·B| ≤ ||A|| * ||B||

chính là biểu hiện hình học của bất đẳng thức. Từ đó, người ta định nghĩa góc giữa hai vectơ và giải thích vì sao hai vectơ càng “cùng hướng” thì tích vô hướng của chúng càng lớn.

Điều này không chỉ mang tính lý thuyết, mà còn được ứng dụng nhiều trong các ngành như đồ họa máy tính, cơ học kỹ thuật, và cả trí tuệ nhân tạo – nơi mà việc tính toán khoảng cách và độ tương tự giữa các điểm dữ liệu là rất quan trọng.

Trong phân tích dữ liệu và máy học

Ngày nay, bất đẳng thức còn được ứng dụng trong việc tính cosine similarity – một phương pháp đo độ tương đồng giữa hai vector trong không gian nhiều chiều. Đây là nền tảng cho các thuật toán gợi ý sản phẩm, tìm kiếm văn bản, hoặc phân tích ngôn ngữ tự nhiên.

Ngoài ra, các kỹ thuật phân rã ma trận, PCA (Phân tích thành phần chính), đều dựa một phần vào tư tưởng của bất đẳng thức này nhằm đánh giá mối quan hệ giữa các đại lượng biến thiên trong không gian dữ liệu lớn.

Bất đẳng thức Bunhiacopxki là một trong những công cụ mạnh mẽ và hữu ích nhất trong toán học, từ bài tập học sinh đến ứng dụng công nghệ hiện đại. Không chỉ giúp chứng minh các biểu thức đại số, nó còn mở rộng ra các lĩnh vực hình học, giải tích, và xử lý dữ liệu. Khi hiểu đúng và sử dụng thành thạo, bạn sẽ thấy rằng đây là một bất đẳng thức vừa đẹp về mặt toán học, vừa thực tiễn trong nhiều lĩnh vực nghiên cứu và ứng dụng.