Nhị Thức Newton Là Gì? Công Thức, Cách Áp Dụng Chi Tiết

Nhị thức Newton là công thức quan trọng, giúp khai triển biểu thức dạng  (a+b)ⁿ  thành một chuỗi các hạng tử. Với ứng dụng rộng rãi trong nhiều lĩnh vực toán học như xác suất và tổ hợp, định lí Newton không chỉ đơn giản hóa các phép toán mà còn là phương pháp giải quyết các vấn đề hiệu quả.

Lý thuyết về nhị thức Newton

Định lý khai triển nhị thức Newton

Định lý Newton là một định lý toán học về việc khai triển hàm mũ của tổng. Định lý khai triển một nhị thức bậc n thành một đa thức n+1 số hạng có dạng:

(a+b)ⁿ=∑ⁿₖ₌₀Cᴷₙaⁿ⁻ᴷbᴷ= ∑ⁿₖ₌₀Cᴷₙaᴷbⁿ⁻ᴷ

Có (Cⁿₖ) còn được gọi là số tổ hợp chập k của n phần tử (0≤k≤n). Ta có định lý, số các tổ hợp chập k của n phần tử đã cho như sau:

Lý thuyết về nhị thức Niu tơn

Công thức nhị thức Niu tơn

Với ∀n∈N* với cặp số (a,b) ta có:

(a+b)ⁿ=∑ⁿₖ₌₀Cᴷₙaⁿ⁻ᴷbᴷ= C⁰ₙaⁿ + C¹ₙaⁿ⁻¹b + C²ₙaⁿ⁻²b²+...+ Cᵐₙbⁿ

(a-b)ⁿ=∑ⁿₖ₌₀(-1)ᴷCᴷₙaⁿ⁻ᴷbᴷ= C⁰ₙaⁿ - C¹ₙaⁿ⁻¹b + C²ₙaⁿ⁻²b²-...+ (-1)ⁿCᵐₙbⁿ

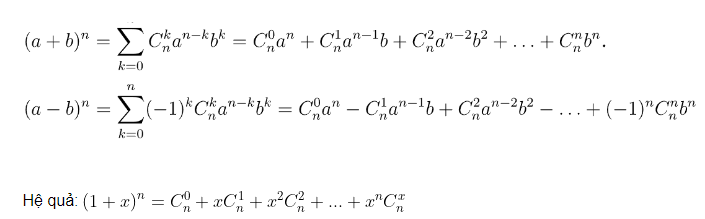
Công thức khai triển nhị thức

Hệ quả:

(1 + x)ⁿ= C⁰ₙ+ xC¹ₙ + x²C²ₙ+...+ xⁿCˣₙ

Ví Dụ Minh Họa

Để hiểu rõ hơn về công thức nhị thức Niu ton, hãy xem xét ví dụ sau:

Khai triển (x + y)³:

(x + y)3 = 3C0 . x³ . y⁰ + 3C1 . x² . y¹ + 3C2 . x¹ . y² + 3C3 . x⁰ . y³

= x +³3x²y + 3xy² + y³

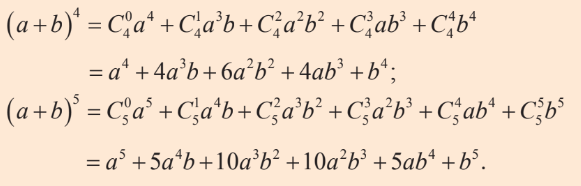
Ví dụ khai triển theo nhị thức Niu tơn

Ứng dụng của định lý Newton

Công thức nhị thức Niu tơn có nhiều ứng dụng trong các lĩnh vực khác nhau trong cuộc sống. Dưới đây là một số ứng dụng phổ biến: 

Trong Toán Học

Giải phương trình: Công thức nhị thức giúp giải quyết các bài toán phương trình đa thức phức tạp bằng cách khai triển và đơn giản hóa lại chúng.

Chuỗi vô hạn: Nhị thức Niu tơn là nền tảng cho việc phát triển các chuỗi vô hạn, nhất  là trong giải tích.

Trong Vật Lý

Cơ Học Lượng Tử: Công thức nhị thức Niu tơn được dùng để tính toán xác suất và các hàm sóng trong cơ học lượng tử.

Động Lực Học: Giúp mô hình hóa và giải quyết các bài toán liên quan đến động lực học phức tạp.

Trong Thống Kê

Phân Phối Xác Suất: Công thức nhị thức cũng là cơ sở cho phân phối nhị thức Đây cũng là một trong những phân phối xác suất quan trọng nhất.

Phân Tích Dữ Liệu: Giúp phân tích và dự đoán các xu hướng dữ liệu trong các nghiên cứu thống kê.

Cách tính hệ số của Nhị Thức

Hệ số nhị thức là một phần quan trọng áp dụng trong công thức nhị thức Newton. Để tính hệ số nhị thức nCk, ta cần dùng công thức:

nCk = n! / (k! .(n-k)!)

Trong đó n! (giai thừa của n) tức là tích của tất cả các số nguyên dương từ 1 đến n. Ví dụ:  5! = 5 . 4 . 3 . 2 . 1 = 120.

Ví Dụ Tính Hệ Số của Nhị Thức sau:  Tính 5C2?

5C2 = 5! / (2! . (5-2)!) = 120 / (2 . 6) = 10
 

Phương pháp phân tích và chứng minh Công Thức

Để hiểu rõ hơn về công thức nhị thức Niu tơn, ta cần phân tích và chứng minh nó. Công thức này được dùng để chứng minh bằng phương pháp quy nạp toán học hoặc dùng định lý tổ hợp.

Chứng minh bằng phương pháp Quy Nạp Toán Học

Phương pháp quy nạp toán học là một công cụ phổ biến dùng để chứng minh các định lý toán học. Để chứng minh công thức nhị thức Niu tơn bằng quy nạp, ta cần thực hiện các bước sau:

Bước 1: Cơ Sở Quy Nạp – Chứng minh công thức này đúng với n = 1.

Bước 2: Giả Thiết Quy Nạp – Giả sử công thức này đúng với n = k.

Bước 3: Bước Quy Nạp – Chứng minh công thức trên đúng với n = k + 1 dựa trên giả thiết quy nạp.

Chứng Minh bằng định lí Tổ Hợp

Công thức nhị thức Niu tơn cũng có thể được chứng minh bằng cách áp dụng định lý tổ hợp. Tức là dựa trên việc đếm số cách chọn k phần tử từ n phần tử.

 

Những thách thức và lưu ý khi sử dụng nhị thức Niu tơn

Mặc dù công thức nhị thức Newton là rất hữu ích. Tuy nhiên việc áp dụng nó cũng có thể gặp một số thách thức, nhất là khi làm việc với các số mũ lớn hay trong các biểu thức phức tạp.

Độ Phức Tạp Tính Toán: Khi n lớn thì việc tính toán các hệ số nhị thức và khai triển cũng có thể trở nên phức tạp và tốn thời gian.

Sai Số Tính Toán: Trong các ứng dụng thực tế, sai số tính toán cũng có thể xảy ra. Đặc biệt là khi phải làm việc với các số thập phân hoặc số phức.

 

Các dạng toán nhị thức Niu tơn

Dạng 1: Tìm hệ số trong khai triển và tìm số hạng trong khai triển

Với dạng bài toán này, áp dụng số hạng tổng quát (số hạng thứ k+1) của khai triển. Tiếp đó biến đổi để tách riêng phần biến và phần hệ số. Sau đó kết hợp đề bài để xác định chỉ số k. Lưu ý rằng số hạng gồm hệ số + phần biến.

Ví dụ 1: Tìm hệ số trong khai triển sau

Hệ số x³¹ trong khai triển (x +1/x²)⁴⁰ là bao nhiêu?

Lời giải:

(x +1/x²)⁴⁰ =∑⁴⁰ₖ₌₀Cᵏ₄₀xᵏ. (1/x²)⁴⁰⁻ᵏ=∑⁴⁰ₖ₌₀Cᵏ₄₀.x³ᴷ⁻⁸⁰

Hệ số của x³¹ là Cᵏ₄₀ với k thỏa mãn điều kiện 3k-80=31=> k=37

Vệ hệ số của x³¹  là C³⁷₄₀= 9880

Ví dụ 2: Tìm số hạng trong khai triển.

Tìm số hạng không có x trong khai triển nhị thức sau:

(x + 1/x)¹²

Lời giải:

Số hạng tổng quát trong khai triển (x + 1/x)¹² là Cᵏ₁₂x¹²⁻ᴷ1/xᵏ= Cᵏ₁₂x¹²⁻²ᵏ

Số hạng không có x ứng với k thỏa mãn điều kiện: 12-2k=0=> k=6

Số hạng không chứa x là C⁶₁₂ = 924

 

Dạng 2: Rút gọn đẳng thức, chứng minh biểu thức

Cách giải:

Nhận xét bài toán từ đó chọn hàm số phù hợp với tổng đẳng thức, bất đẳng thức. Thông thường ta hay dùng hàm cơ bản (x+1)ⁿ, (1+x)ⁿ, (1-x)ⁿ, (x-1)ⁿ

Khai triển nhị thức vừa tìm được và dùng phép biến đổi đại số, giải tích để có dạng phù hợp với đề bài.

Chọn giá trị x sao cho phù hợp với biểu thức như đề bài. Thông thường chọn x là các số 1 hay -1.

Khi đó ta có được tổng hay mệnh đề cần chứng minh.

Ví dụ : Rút gọn đẳng thức

Tính tổng S= C⁰₃₀₃₀ - 2C¹₃₀₃₀+ 2²C²₃₀₃₀- 2³C³₃₀₃₀+...+3³⁰³⁰C³⁰³⁰₃₀₃₀

Lời giải:

Theo công thức nhị thức Niu tơn với a=1, b=-2 ta có:

(1-2)³⁰³⁰= C⁰₃₀₃₀ - 2C¹₃₀₃₀+ 2²C²₃₀₃₀- 2³C³₃₀₃₀+...+3³⁰³⁰C³⁰³⁰₃₀₃₀= 1

Ngoài ra còn một số dạng bài khác, các em có thể tham khảo thêm.